谣言止于无为
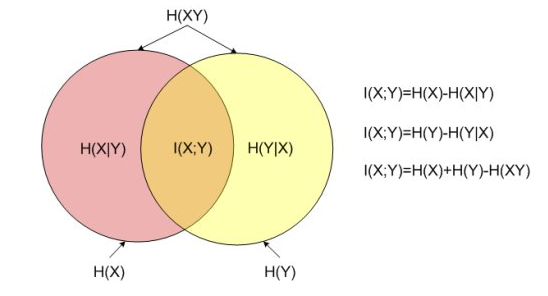
概率分析证明 , 谣言止于无为 。 设命题X为疑似谣言 , 其真值为p(x) , Y为与X不一致的命题 , Y真值为p(y) , X与Y同时成立的概率为p(x,y) , 则根据Shannon理论 , 当已知X时判断Y究竟能否成立的互信息量I(X,Y)必满足下列条件: 1)在X与Y为离散随机变量的情形下 , 有
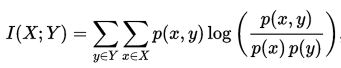
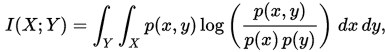

推荐阅读
- 胜任力测评■盘点 | 2019关于儿童的八大谣言,你信了哪一个?
- 「沈阳」沈阳将建设五环?别信!这是中介在散布谣言!
- #系谣言#牡丹江市4月13日起封城?官方:系谣言 已查到造谣者
- 广州警方:“广州1000多外籍人员核酸检测阳性”为谣言
- 广州两名外籍人员带病逃脱?警方:系谣言
- #胥女士#莫名成了超市小偷,微信群里这些消息让她崩溃!微话题:如何打击网络谣言?
- 『我爱金胶州』胶州警方提醒:制造、传播谣言,须承担法律责任!
- 刘某■本想种点罂粟治病,却因听信谣言受处罚
- 「广州」广州将建方舱医院?谣言
- [广州瑶台封村]广州瑶台“封村”?建方舱医院?广州警方查处谣言发布者