еҲқдёӯж•°еӯҰв–ІеҲҶдә«дёҖйҒ“йҡҫеәҰиҫғеӨ§зҡ„еҲқдёӯж•°еӯҰйўҳпјҢдёҚе°‘еӯҰз”ҹзӣҙжҺҘж”ҫејғпјҢиҫ…еҠ©зәҝеҫҲйҮҚиҰҒ
ж–Үз« еӣҫзүҮ
еҗ„дҪҚжңӢеҸӢ пјҢ еӨ§е®¶еҘҪпјҒд»ҠеӨ©жҳҜ2020е№ҙ5жңҲ12ж—ҘжҳҹжңҹдәҢ гҖӮ ж•°еӯҰдё–з•Ңе°Ҷ继з»ӯеҸ‘еёғеҲқдёӯж•°еӯҰд№ йўҳеҸҠи§Јжһҗ пјҢ еҰӮжһңдҪ жҳҜжқҘеҲ°иҝҷйҮҢзҡ„ж–°жңӢеҸӢ пјҢ еҸҜд»Ҙзҝ»зңӢж•°еӯҰдё–з•Ңд»ҘеүҚеҸ‘еёғзҡ„ж–Үз« гҖӮ 笔иҖ…еёҢжңӣеҜ№е№ҝеӨ§еӯҰз”ҹзҡ„еӯҰд№ е’ҢеӨҮиҖғжңүдёҖдәӣеё®еҠ© пјҢ иҜ·жңӢеҸӢ们еҜҶеҲҮе…іжіЁж•°еӯҰдё–з•ҢпјҒ
д»ҠеӨ© пјҢ ж•°еӯҰдё–з•ҢдёәеӨ§е®¶еҲҶдә«дёҖйҒ“еҲқдёӯж•°еӯҰдёӯйҡҫеәҰиҫғеӨ§гҖҒз»јеҗҲжҖ§ејәзҡ„и§Јзӯ”йўҳ пјҢ иҝҷйўҳйҡҫеәҰиҖғжҹҘеҗҢеӯҰ们зҡ„з»јеҗҲиғҪеҠӣ пјҢ еұһдәҺжӢ”й«ҳйўҳеһӢ гҖӮ еӨ§е®¶еңЁеҒҡйўҳж—¶иҰҒи®Өзңҹи§ӮеҜҹеӣҫеҪў пјҢ е……еҲҶеҲ©з”Ёе·ІзҹҘжқЎд»¶ пјҢ иҝҳиҰҒиҖғиҷ‘дҪңиҫ…еҠ©зәҝ пјҢ еҸӘжңүиҝҷж ·жүҚеҸҜиғҪеҫҲеҝ«еҒҡеҮәжқҘ гҖӮ иҜ·еӨ§е®¶е…ҲзӢ¬з«ӢжҖқиҖғдёҖдјҡе„ҝ пјҢ еҶҚзңӢдёӢйқўзҡ„еҲҶжһҗе’Ңи§Јзӯ”иҝҮзЁӢ пјҢ зӣёдҝЎдёҖе®ҡдјҡжңү收иҺ·пјҒ
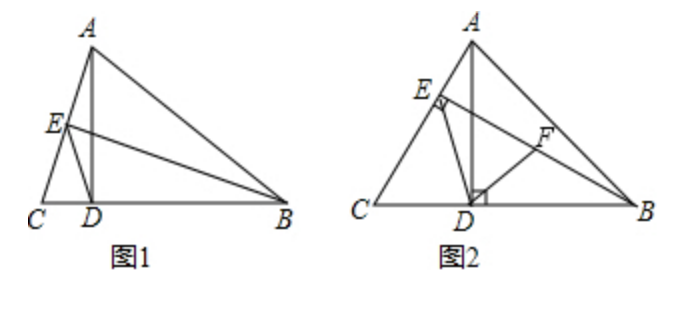
дҫӢйўҳпјҡпјҲеҲқдёӯж•°еӯҰз»јеҗҲйўҳпјүеҰӮеӣҫ1жүҖзӨә пјҢ е·ІзҹҘеңЁв–іABCдёӯ пјҢ BEвҠҘACдәҺзӮ№E пјҢ ADвҠҘBCдәҺзӮ№D пјҢ иҝһжҺҘDE.
пјҲ1пјүиӢҘAB=BC пјҢ DE=1 пјҢ BE=3 пјҢ жұӮв–іABCзҡ„е‘Ёй•ҝпјӣ
пјҲ2пјүеҰӮеӣҫ2жүҖзӨә пјҢ иӢҘAB=BC пјҢ AD=BD пјҢ вҲ ADBзҡ„и§’е№іеҲҶзәҝDFдәӨBEдәҺзӮ№F пјҢ жұӮиҜҒпјҡBF=вҲҡ2 DEпјҺ
иҝҷйҒ“йўҳзҡ„йҡҫеәҰиҫғеӨ§ пјҢ йңҖиҰҒиҫғејәзҡ„еҲҶжһҗжҺЁзҗҶиғҪеҠӣ гҖӮ еҫҲеӨҡеҗҢеӯҰз”ұдәҺзјәд№ҸеҲҶжһҗй—®йўҳзҡ„иғҪеҠӣ пјҢ дёҚиғҪеҸ‘зҺ°йўҳдёӯиҖғжҹҘеҲ°зҡ„зҹҘиҜҶзӮ№ пјҢ иҖҢеҜјиҮҙж— жі•е®ҢжҲҗ гҖӮ 第дёҖй—®иҝҳжҜ”иҫғз®ҖеҚ• пјҢ еӨ§еӨҡж•°дәәеә”иҜҘеҸҜд»ҘеҒҡеҮәжқҘ гҖӮ 第дәҢй—®зҡ„йҡҫеәҰе°ұеҫҲеӨ§дәҶ пјҢ иҰҒд»”з»ҶеҲҶжһҗеӣҫеҪў пјҢ 并结еҗҲе·ІзҹҘжқЎд»¶ пјҢ йңҖиҰҒйҖҡиҝҮдҪңиҫ…еҠ©зәҝ пјҢ иҜҒжҳҺдёүи§’еҪўе…ЁзӯүжүҚиғҪеҫ—еҮәз»“и®ә гҖӮ
еӨ§е®¶еңЁи§Јзӯ”жӯӨйўҳж—¶ пјҢ иҰҒзҶҹз»ғиҝҗз”Ёе…Ёзӯүдёүи§’еҪўзҡ„жҖ§иҙЁдёҺеҲӨе®ҡ пјҢ д»ҘеҸҠзӯүи…°дёүи§’еҪўдёҺзӣҙи§’дёүи§’еҪўзӯүзҹҘиҜҶ гҖӮ дёӢйқў пјҢ ж•°еӯҰдё–з•Ңе°ұдёҺеӨ§е®¶дёҖиө·жқҘи§ЈеҶіиҝҷйҒ“дҫӢйўҳеҗ§пјҒ
еҲҶжһҗпјҡпјҲ1пјүз”ұзӣҙи§’дёүи§’еҪўж–ңиҫ№дёҠзҡ„дёӯзәҝжҖ§иҙЁеҸҜд»Ҙеҫ—еҮәDE=1/2AC=AE пјҢ жүҖд»ҘAC=2DE=2 пјҢ AE=1 пјҢ еҶҚз”ұеӢҫиӮЎе®ҡзҗҶжұӮеҮәABе’ҢBCзҡ„й•ҝ пјҢ еҚіеҸҜеҫ—еҮәз»“жһңпјӣ
пјҲ2пјүиҝһжҺҘAFпјҲеҰӮеӣҫ2жүҖзӨәпјү пјҢ з”ұзӯүи…°дёүи§’еҪўзҡ„жҖ§иҙЁеҫ—еҮәвҲ 3=вҲ 4 пјҢ з»“еҗҲв–іABDжҳҜзӯүи…°зӣҙи§’дёүи§’еҪў пјҢ еҫ—еҮәвҲ DAB=вҲ DBA=45В° пјҢ вҲ 3=22.5В° пјҢ з”ұSASиҜҒжҳҺв–іADFвүҢв–іBDF пјҢ еҫ—еҮәAF=BF пјҢ вҲ 2=вҲ 3=22.5В° пјҢ еҶҚиҜҒеҮәв–іAEFжҳҜзӯүи…°зӣҙи§’дёүи§’еҪў пјҢ еҚіеҸҜеҫ—еҮәз»“и®әпјҺ
пјҲ1пјүи§ЈпјҡвҲөAB=BC пјҢ BEвҠҘAC пјҢ
вҲҙAE=CE пјҢ вҲ AEB=90В° пјҢ
вҲөADвҠҘBC пјҢ
вҲҙвҲ ADC=90В° пјҢ
вҲҙDE=1/2AC=AE пјҢ
вҲҙAC=2DE=2 пјҢ AE=1 пјҢ
еңЁзӣҙи§’дёүи§’еҪўAEBдёӯ пјҢ
AB^2=AE^2+BE^2 пјҢ BE=3 пјҢ
вҲҙAB=вҲҡ10 пјҢ
вҲҙBC=вҲҡ10 пјҢ
вҲҙв–іABCзҡ„е‘Ёй•ҝдёә
AB+BC+AC=2вҲҡ10 +2пјӣ
гҖҗеҲқдёӯж•°еӯҰв–ІеҲҶдә«дёҖйҒ“йҡҫеәҰиҫғеӨ§зҡ„еҲқдёӯж•°еӯҰйўҳпјҢдёҚе°‘еӯҰз”ҹзӣҙжҺҘж”ҫејғпјҢиҫ…еҠ©зәҝеҫҲйҮҚиҰҒгҖ‘пјҲ2пјүиҜҒжҳҺпјҡиҝһжҺҘAF пјҢ еҰӮеӣҫ2жүҖзӨә пјҢ
вҲөAB=BC пјҢ BEвҠҘAC пјҢ
вҲҙвҲ 3=вҲ 4 пјҢ
вҲөвҲ ADC=вҲ ADB=90В° пјҢ AD=BD пјҢ
вҲҙв–іABDжҳҜзӯүи…°зӣҙи§’дёүи§’еҪў пјҢ
вҲҙвҲ DAB=вҲ DBA=45В° пјҢ
вҲҙвҲ 3=22.5В° пјҢ
вҲөвҲ 1+вҲ C=вҲ 3+вҲ C=90В° пјҢ
вҲҙвҲ 1=вҲ 3=22.5В° пјҢ
вҲөDFе№іеҲҶвҲ ADB пјҢ
вҲҙвҲ ADF=вҲ BDF пјҢ
еңЁв–іADFе’Ңв–іBDFдёӯ пјҢ
вҲөAD=BD пјҢ вҲ ADF=вҲ BDF пјҢ DF=DF пјҢ
вҲҙв–іADFвүҢв–іBDFпјҲSASпјү пјҢ
вҲҙAF=BF пјҢ вҲ 2=вҲ 3=22.5В° пјҢ
вҲҙвҲ EAF=вҲ 1+вҲ 2=45В° пјҢ
вҲҙв–іAEFжҳҜзӯүи…°зӣҙи§’дёүи§’еҪў пјҢ
вҲҙAF=вҲҡ2 AE пјҢ
вҲөDE=AE пјҢ AF=BF пјҢ
вҲҙBF=вҲҡ2 DEпјҺ
пјҲе®ҢжҜ•пјү
иҝҷйҒ“йўҳдё»иҰҒиҖғжҹҘдәҶеӢҫиӮЎе®ҡзҗҶгҖҒе…Ёзӯүдёүи§’еҪўзҡ„еҲӨе®ҡдёҺжҖ§иҙЁгҖҒзӯүи…°зӣҙи§’дёүи§’еҪўзҡ„еҲӨе®ҡдёҺжҖ§иҙЁгҖҒзӣҙи§’дёүи§’еҪўж–ңиҫ№дёҠзҡ„дёӯзәҝжҖ§иҙЁзӯүзҹҘиҜҶ гҖӮ жң¬йўҳйҡҫеәҰиҫғеӨ§ пјҢ з»јеҗҲжҖ§ејә пјҢ йңҖиҰҒйҖҡиҝҮдҪңиҫ…еҠ©зәҝиҝӣиЎҢеҲҶжһҗжҺЁзҗҶ гҖӮ жё©йҰЁжҸҗзӨәпјҡжңӢеҸӢ们еҰӮжһңжңүдёҚжҳҺзҷҪд№ӢеӨ„жҲ–иҖ…жңүжӣҙеҘҪзҡ„и§Јйўҳж–№жі• пјҢ ж¬ўиҝҺеӨ§е®¶еңЁдёӢйқўз•ҷиЁҖи®Ёи®ә гҖӮ и°ўи°ўпјҒ
жҺЁиҚҗйҳ…иҜ»
- в–ІеҲқдёӯз”ҹдёҚеә”иҜҘжңүжүӢжңәпјҹзҸӯдё»д»»пјҡдёҚиғҪеҸӘзңӢеқҸеӨ„пјҢжІЎжүӢжңәзҡ„еӯ©еӯҗеҗғеӨ§дәҸ
- гҖҺиҖғиҜ•гҖҸиҖғеүҚзҙ§еј еҲ°зқЎдёҚзқҖпјҹй«ҳдёүиҖҒеёҲеҲҶдә«ж”ҫжқҫж–№жі•пјҢиҖғз”ҹиҖғеүҚеҝ…еӨҮ
- гҖҢзү©зҗҶгҖҚзү©зҗҶиҖҒеёҲжҖ»з»“пјҡеҲқдёӯвҖңеҺӢеҠӣе’ҢеҺӢејәвҖқиҖғзӮ№и§ЈжһҗжүӢеҶҢпјҒеӨҚд№ еӨҡжӢҝ20еҲҶ
- гҖҺзү©зҗҶгҖҸеҲқдёӯзү©зҗҶеёёиҜҶйўҳеҗҲйӣҶж•ҙзҗҶеҫҲе…ЁйқўпјҢе»әи®®еҲқдёӯз”ҹйғҪдҝқз•ҷдёҖд»ҪпјҒ
- еҲқдёӯж•°еӯҰ@еҲқдёӯж•°еӯҰдёЁеҠЁзӮ№жңҖеҖјй—®йўҳ19еӨ§жЁЎеһӢ+дҫӢйўҳиҜҰи§ЈпјҢеҪ»еә•и§ЈеҶіеҺӢиҪҙйҡҫйўҳ
- гҖҢж•°еӯҰгҖҚиҝҷ3дёӘеӨ§еӯҰдё“дёҡжҢӮ科зҺҮеҫҲй«ҳпјҢжҜ•дёҡеҗҺиҝҳеҫҲйҡҫжүҫе·ҘдҪңпјҢжҠҘиҖғиҰҒж…ҺйҮҚ
- дёӯиҖғ@иҝҳеңЁеҒҡиҝҷ4з§ҚвҖңж— з”ЁеҠҹвҖқзҡ„еҲқдёӯз”ҹпјҢзҸӯдё»д»»пјҡеҸҜиғҪж— зјҳеҘҪй«ҳдёӯ
- гҖҢдёӯе°ҸеӯҰгҖҚдёәд»Җд№ҲиЎҘиҜҫе’ҢдёҚиЎҘиҜҫзҡ„еҲқдёӯз”ҹпјҢеҚҮе…Ҙй«ҳдёӯеҗҺе·®и·қеҫҲеӨ§пјҹеҺҹеӣ жңү3зӮ№пјҒ
- ж•°еӯҰпјҡй«ҳиҖғеЎ«еҝ—ж„ҝж—¶пјҢж•°еӯҰе·®зҡ„еӯ©еӯҗжңҖеҘҪйҒҝејҖ3дёӘдё“дёҡпјҢеҲ«з»ҷиҮӘе·ұвҖңж·»е өвҖқ
- гҖҗзҗҶз»јгҖ‘з»ҸйӘҢеҲҶдә«пјҡй«ҳиҖғз”ҹеҰӮдҪ•дҝқиҜҒ50еҲҶй’ҹеҶ…жҠҠзҗҶз»јйҖүжӢ©йўҳ126еҲҶе…ЁеҒҡеҜ№