е“Ҙеҫ·е·ҙиө«зҢңжғіжқҘжәҗгҖҒд»Ӣз»Қе’ҢиҜҒжҳҺжғ…еҶөдёҺpythonе®һзҺ°
1 иҜҙжҳҺ
=====
1.1 е“Ҙеҫ·е·ҙиө«зҢңжғізҡ„жқҘжәҗгҖҒд»Ӣз»Қе’ҢиҜҒжҳҺжғ…еҶө гҖӮ
1.2 pythonе®һзҺ° гҖӮ
1.3 иө„ж–ҷжқҘжәҗпјҡ
#360зҷҫ科2 е“Ҙеҫ·е·ҙиө«зҢңжғі
===========
2.1 е“Ҙеҫ·е·ҙиө«пјҲ1690.3.18-1764.11.20пјүпјҡжҳҜеҫ·еӣҪж•°еӯҰ家 гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еӣҫзүҮжқҘиҮӘпјҡ360зҷҫ科 пјҢ д»…дҫӣеӯҰд№ пјҢ еҰӮжңүдҫөжқғиҜ·иҒ”зі» пјҢ е®ҡеҲ
2.2 жқҘжәҗпјҡ
е“Ҙеҫ·е·ҙиө«1742е№ҙз»ҷ欧жӢүзҡ„дҝЎдёӯе“Ҙеҫ·е·ҙиө«жҸҗеҮәдәҶд»ҘдёӢзҢңжғі:д»»ж„ҸеӨ§дәҺ2зҡ„еҒ¶ж•°йғҪеҸҜеҶҷжҲҗдёӨдёӘиҙЁж•°д№Ӣе’Ң гҖӮ з”ұжӯӨеј•з”іеҮәжқҘзҡ„ гҖӮ
2.3 еҺҹдҝЎпјҡ
#еҸӮиҖғж–Үз« еңЁиҝҷе°ҒдҝЎдёӯ пјҢ е“Ҙеҫ·е·ҙиө«жҸҗеҮәпјҡ
гҖҗе“Ҙеҫ·е·ҙиө«зҢңжғіжқҘжәҗгҖҒд»Ӣз»Қе’ҢиҜҒжҳҺжғ…еҶөдёҺpythonе®һзҺ°гҖ‘пјҲ1пјүд»»дҪ•дёҖдёӘвүҘ6зҡ„еҒ¶ж•° пјҢ йғҪеҸҜд»ҘиЎЁзӨәжҲҗдёӨдёӘеҘҮиҙЁж•°д№Ӣе’Ңпјӣ
пјҲ2пјүд»»дҪ•дёҖдёӘвүҘ9зҡ„еҘҮж•° пјҢ йғҪеҸҜд»ҘиЎЁзӨәжҲҗдёүдёӘеҘҮиҙЁж•°д№Ӣе’Ң гҖӮ
2.4 еҲҶзұ»пјҡ
"ејәе“Ҙеҫ·е·ҙиө«зҢңжғі"пјҡеҚід»»дёҖеӨ§дәҺ2зҡ„еҒ¶ж•°йғҪеҸҜеҶҷжҲҗдёӨдёӘзҙ ж•°д№Ӣе’Ң гҖӮ
д№ҹжҳҜпјҡ"е…ідәҺеҒ¶ж•°зҡ„е“Ҙеҫ·е·ҙиө«зҢңжғі" гҖӮ
==========================
"ејұе“Ҙеҫ·е·ҙиө«зҢңжғі"пјҡд»»дёҖеӨ§дәҺ7зҡ„еҘҮж•°йғҪеҸҜеҶҷжҲҗдёүдёӘиҙЁж•°д№Ӣе’Ң гҖӮ
д№ҹжҳҜпјҡ"е…ідәҺеҘҮж•°зҡ„е“Ҙеҫ·е·ҙиө«зҢңжғі" гҖӮ е°ҡжңӘе®Ңе…Ёи§ЈеҶі гҖӮ
2.5 иҜҒжҳҺжғ…еҶөпјҡ
2.5.1 е“Ҙеҫ·е·ҙиө«е’Ң欧жӢүпјҡиҝҷдёӨдҪҚеӨ§ж•°еӯҰ家еҲ°жӯ»д№ҹжІЎжңүиҜҒжҳҺеҮәжқҘ гҖӮ
2.5.2 з ”з©¶еҒ¶ж•°зҡ„е“Ҙеҫ·е·ҙиө«зҢңжғізҡ„еӣӣдёӘйҖ”еҫ„ гҖӮ иҝҷеӣӣдёӘйҖ”еҫ„еҲҶеҲ«жҳҜ:ж®Ҷзҙ ж•° пјҢ дҫӢеӨ–йӣҶеҗҲ пјҢ е°ҸеҸҳйҮҸзҡ„дёүзҙ ж•°е®ҡзҗҶд»ҘеҸҠеҮ д№Һе“Ҙеҫ·е·ҙиө«й—®йўҳ гҖӮ
ж®Ҷзҙ ж•°е°ұжҳҜзҙ еӣ еӯҗдёӘж•°дёҚеӨҡзҡ„жӯЈж•ҙж•° пјҢ жҳҫ然 пјҢ е“Ҙеҫ·е·ҙиө«зҢңжғіе°ұеҸҜд»ҘеҶҷжҲҗ"1+1" гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
3 pythonе®һзҺ°ејәе“Ҙеҫ·е·ҙиө«зҢңжғі
======================
3.1 жҰӮеҝөпјҡ
иҙЁж•°(prime number)пјҡеҸҲз§°зҙ ж•° пјҢ
жҳҜжҢҮеңЁеӨ§дәҺ1зҡ„иҮӘ然数дёӯ пјҢ йҷӨдәҶ1е’Ңе®ғжң¬иә«д»ҘеӨ–дёҚеҶҚжңүе…¶д»–еӣ ж•°зҡ„иҮӘ然数пјӣеҗҰеҲҷз§°дёәеҗҲж•° гҖӮ
3.2 д»Јз Ғпјҡ
#ејәе“Ҙеҫ·е·ҙиө«зҢңжғі#д»»дҪ•дёҖдёӘеӨ§дәҺ2зҡ„еҒ¶ж•°йғҪжҳҜдёӨдёӘзҙ ж•°д№Ӣе’Ң#иҙЁж•°зҡ„еҲӨе®ҡdef isprime(n): i = 2 while(i
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жіЁж„ҸеӨӘеӨ§дәҶ пјҢ жң¬жңәеҚЎ пјҢ дёҖиҲ¬10дёҮд»ҘдёӢзҡ„еҒ¶ж•°иҝҳеҸҜд»Ҙ
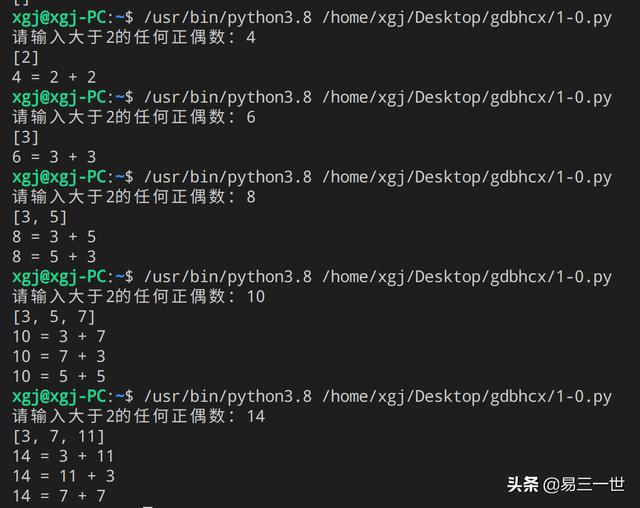
3.4 йӘҢиҜҒејәе“Ҙеҫ·е·ҙиө«зҢңжғізҡ„жӯЈзЎ® пјҢ д»Јз Ғ
#д»»дҪ•дёҖдёӘеӨ§дәҺ2зҡ„еҒ¶ж•°йғҪжҳҜдёӨдёӘзҙ ж•°д№Ӣе’Ң#йӘҢиҜҒејәе“Ҙеҫ·е·ҙиө«зҢңжғіеңЁдёҖе®ҡиҢғеӣҙеҶ…жҳҜеҗҰжӯЈзЎ®#иҙЁж•°зҡ„еҲӨе®ҡdef isprime(num): i = 2 while(i
жҺЁиҚҗйҳ…иҜ»


















