1Tж•°жҚ®еҝ«йҖҹжҺ’еәҸпјҒеҚҒз§Қз»Ҹе…ёжҺ’еәҸз®—жі•жҖ»з»“( е…ӯ )
< min) {min = i;}}//и®Ўз®—жЎ¶зҡ„ж•°йҮҸпјҲеҸҜд»ҘиҮӘе®ҡд№үе®һзҺ°пјүint bucketNumber = (max - min) / array.length + 1;List
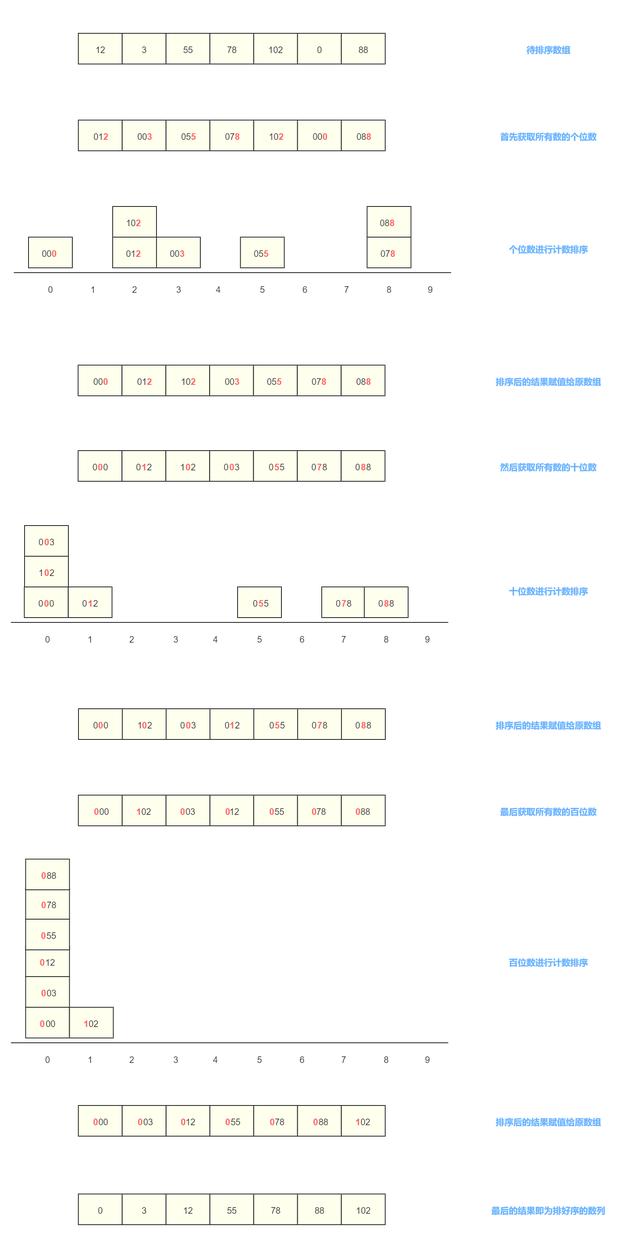
еҹәж•°жҺ’еәҸдёҖиҲ¬жҳҜеҜ№жүҖжңүйқһиҙҹж•ҙж•°иҝӣиЎҢжҺ’еәҸзҡ„ пјҢ дҪҶжҳҜд№ҹеҸҜд»ҘжңүеҲ«зҡ„жүӢж®өжқҘеҺ»жҺүиҝҷз§ҚйҷҗеҲ¶пјҲжҜ”еҰӮйғҪеҠ дёҖдёӘеӣәе®ҡзҡ„ж•°жҲ–иҖ…йғҪд№ҳдёҖдёӘеӣәе®ҡзҡ„ж•° пјҢ жҺ’е®ҢеәҸеҗҺеҶҚжҒўеӨҚзӯүзӯүпјү гҖӮ еҹәж•°жҺ’еәҸе’ҢжЎ¶жҺ’еәҸеҫҲеғҸ пјҢ жЎ¶жҺ’еәҸжҳҜжҢүж•°еҖјзҡ„еҢәй—ҙиҝӣиЎҢеҲ’еҲҶ пјҢ иҖҢеҹәж•°жҺ’еәҸжҳҜжҢүж•°зҡ„дҪҚж•°иҝӣиЎҢеҲ’еҲҶ гҖӮ еҗҢж—¶иҝҷдёӨдёӘжҺ’еәҸйғҪжҳҜйңҖиҰҒдҫқйқ е…¶д»–жҺ’еәҸз®—жі•жқҘе®һзҺ°зҡ„пјҲеҰӮжһңдёҚз®—йҖ’еҪ’и°ғз”ЁжЎ¶жҺ’еәҸжң¬иә«зҡ„иҜқпјү гҖӮ еҹәж•°жҺ’еәҸжҜҸдёҖиҪ®зҡ„еҶ…йғЁжҺ’еәҸдјҡдҪҝз”ЁеҲ°и®Ўж•°жҺ’еәҸжқҘе®һзҺ° пјҢ еӣ дёәжҜҸдёҖдҪҚдёҠзҡ„ж•°еӯ—ж— йқһе°ұжҳҜ0-9 пјҢ жҳҜдёҖдёӘе°ҸиҢғеӣҙзҡ„ж•° пјҢ жүҖд»ҘдҪҝз”Ёи®Ўж•°жҺ’еәҸеҫҲеҗҲйҖӮ гҖӮ
еҹәж•°жҺ’еәҸжү§иЎҢзӨәж„Ҹеӣҫпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
е…·дҪ“зҡ„е®һзҺ°д»Јз ҒеҰӮдёӢпјҡ
public int[] radixSort(int[] array) {if (array == null || array.length < 2) {return array;}//и®°еҪ•еҫ…жҺ’еәҸж•°з»„дёӯзҡ„жңҖеӨ§еҖјint max = array[0];for (int i : array) {if (i > max) {max = i;}}//иҺ·еҸ–жңҖеӨ§еҖјзҡ„дҪҚж•°int maxDigits = 0;while (max != 0) {max /= 10;maxDigits++;}//з”ЁжқҘи®Ўж•°жҺ’еәҸзҡ„дёҙж—¶ж•°з»„int[] temp = new int[10];//з”ЁжқҘеӯҳж”ҫжҜҸиҪ®жҺ’еәҸеҗҺзҡ„з»“жһңint[] sortedArray = new int[array.length];for (int d = 1; d <= maxDigits; d++) {//жҜҸж¬ЎеҫӘзҺҜејҖе§ӢеүҚйғҪиҰҒжё…з©әtempж•°з»„дёӯзҡ„еҖјreplaceArray(temp, null);//и®°еҪ•жҜҸдёӘж•°еҮәзҺ°зҡ„ж¬Ўж•°for (int a : array) {temp[getNumberFromDigit(a, d)]++;}//е°Ҷtempж•°з»„иҝӣиЎҢиҪ¬жҚў пјҢ и®°еҪ•жҜҸдёӘж•°еңЁжңҖеҗҺжҺ’еҘҪеәҸзҡ„ж•°з»„дёӯеә”иҜҘиҰҒеӯҳж”ҫзҡ„дҪҚзҪ®+1пјҲеҰӮжһңжңүйҮҚеӨҚзҡ„е°ұи®°еҪ•жңҖеҗҺдёҖдёӘпјүfor (int j = 1; j < temp.length; j++) {temp[j] += temp[j - 1];}//иҝҷйҮҢеҝ…йЎ»жҳҜд»ҺеҗҺеҫҖеүҚйҒҚеҺҶ пјҢ д»ҘжӯӨжқҘдҝқиҜҒзЁіе®ҡжҖ§for (int i = array.length - 1; i >= 0; i--) {int index = getNumberFromDigit(array[i], d);sortedArray[temp[index] - 1] = array[i];temp[index]--;}//дёҖиҪ®и®Ўж•°жҺ’еәҸиҝҮеҗҺ пјҢ е°Ҷиҝҷж¬ЎжҺ’еҘҪеәҸзҡ„з»“жһңиөӢеҖјз»ҷеҺҹж•°з»„replaceArray(array, sortedArray);}return array;}private final static int[] sizeTable = {1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000};/** * иҺ·еҸ–жҢҮе®ҡдҪҚж•°дёҠзҡ„ж•°еӯ—жҳҜеӨҡе°‘ */private int getNumberFromDigit(int number, int digit) {if (digit < 0) {return -1;}return (number / sizeTable[digit - 1]) % 10;}private void replaceArray(int[] originalArray, int[] replaceArray) {if (replaceArray == null) {for (int i = 0; i
жҺЁиҚҗйҳ…иҜ»
- иҘҝйғЁж•°жҚ®еңЁCES 2021жҺЁеҮәеӨҡж¬ҫ4TBе®№йҮҸзҡ„ж——иҲ°зә§SSD
- WhatsApp收йӣҶз”ЁжҲ·ж•°жҚ®ж–°ж”ҝжғ№дј—жҖ’пјҢвҖңеҲ йҷӨWhatsAppвҖқеңЁеңҹиҖіе…¶дёҠзғӯжҗң
- вҖңеҚғеә—еҗҢејҖвҖқеј•иҙЁйҮҸжӢ…еҝ§пјҢе°Ҹзұіеӣһеә”
- жңӘжқҘжғіиҝӣе…ҘAIйўҶеҹҹпјҢиҜҘеӯҰд№ PythonиҝҳжҳҜJavaеӨ§ж•°жҚ®ејҖеҸ‘
- дјҒдёҡ|жҠҖжңҜеҝ«йҖҹиҝӯд»ЈеҖ’йҖјзҹҘиҜҶдә§жқғвҖңиҙҙиә«вҖқжңҚеҠЎпјҢдёҠжө·йҰ–家AIе•Ҷж Үе“ҒзүҢжҢҮеҜјз«ҷе…Ҙй©»еҫҗжұҮиҘҝеІё
- й»‘е®ўзӘғеҸ–250дёҮдёӘдәәж•°жҚ® ж„ҸеӨ§еҲ©иҝҗиҗҘе•ҶжҸҗйҶ’з”ЁжҲ·е°Ҫеҝ«жӣҙжҚўSIMеҚЎ
- йҳізӢ®жҠҘе‘Ҡпјҡ4жҲҗеҸ—и®ҝиҖ…и®ӨдёәиҮӘе·ұзҡ„ж•°жҚ®жҜ”е…Қиҙ№жңҚеҠЎжӣҙжңүд»·еҖј
- дёӯж¶ҲеҚҸзӮ№еҗҚеӨ§ж•°жҚ®зҪ‘з»ңжқҖзҶҹ еҸҚеҜ№еҲ©з”Ёж¶Ҳиҙ№иҖ…дёӘдәәж•°жҚ®з”»еғҸ
- еӯҰд№ еӨ§ж•°жҚ®жҳҜеҗҰйңҖиҰҒеӯҰд№ JavaEE
- ж„ҸеӨ§еҲ©иҝҗиҗҘе•ҶHo Mobileиў«жӣқж•°жҚ®жі„йңІ

















