江苏龙网

  1. 首页 > 人文 > >

二叉树：合并两个二叉树

需要一起操作两个二叉树了
617.合并二叉树【二叉树：合并两个二叉树】给定两个二叉树 ， 想象当你将它们中的一个覆盖到另一个上时 ， 两个二叉树的一些节点便会重叠 。
你需要将他们合并为一个新的二叉树 。 合并的规则是如果两个节点重叠 ， 那么将他们的值相加作为节点合并后的新值 ， 否则不为 NULL 的节点将直接作为新二叉树的节点 。
示例 1:
二叉树：合并两个二叉树文章插图
注意: 合并必须从两个树的根节点开始 。
思路相信这道题目很多同学疑惑的点是如何同时遍历两个二叉树呢？
其实和遍历一个树逻辑是一样的 ， 只不过传入两个树的节点 ， 同时操作 。
递归二叉树使用递归 ， 就要想使用前中后哪种遍历方式？
「本题使用哪种遍历都是可以的！」
我们下面以前序遍历为例 。
动画如下：
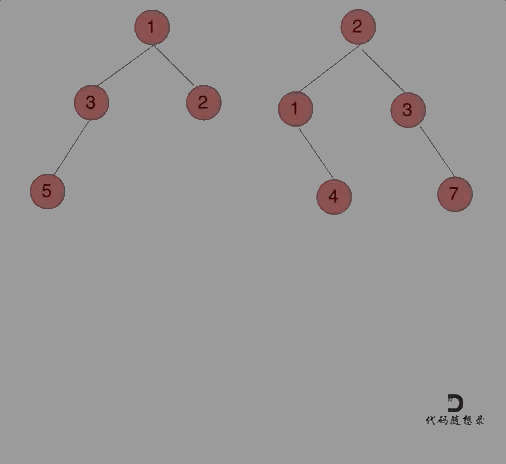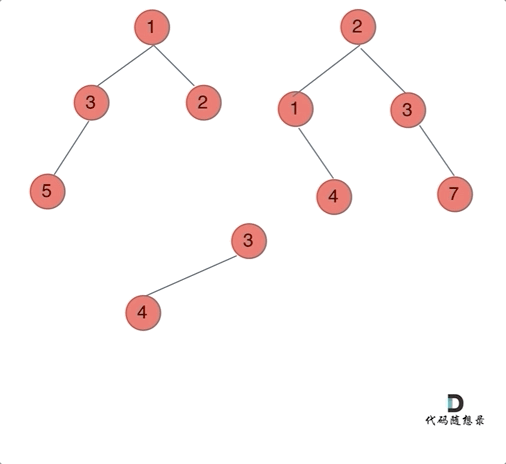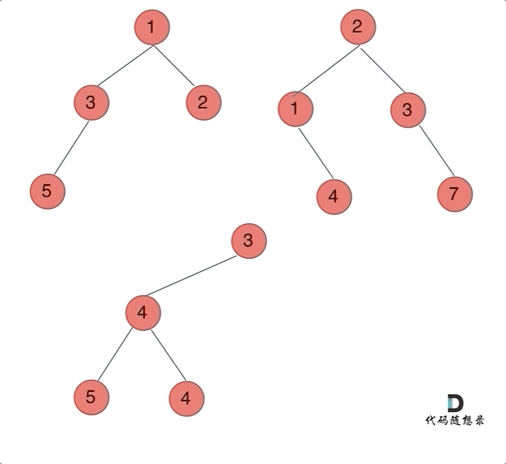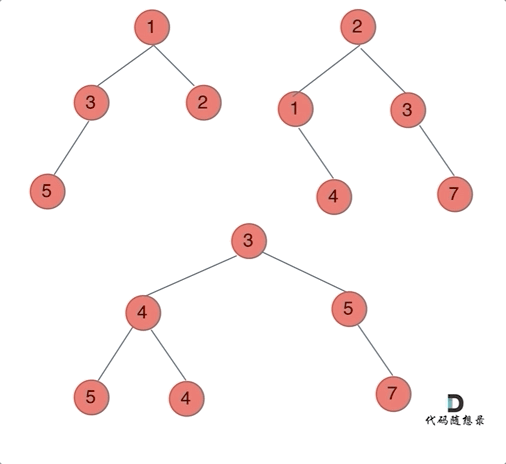二叉树：合并两个二叉树文章插图
那么我们来按照递归三部曲来解决：

  1. 确定递归函数的参数和返回值：
首先那么要合入两个二叉树 ， 那么参数至少是要传入两个二叉树的根节点 ， 返回值就是合并之后二叉树的根节点 。
代码如下：
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
  1. 确定终止条件：
因为是传入了两个树 ， 那么就有两个树遍历的节点t1 和 t2 ， 如果t1 == NULL 了 ， 两个树合并就应该是 t2 了啊（如果t2也为NULL也无所谓 ， 合并之后就是NULL） 。
反过来如果t2 == NULL ， 那么两个数合并就是t1（如果t1也为NULL也无所谓 ， 合并之后就是NULL） 。
代码如下：
if (t1 == NULL) return t2; // 如果t1为空 ， 合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空 ， 合并之后就应该是t1
  1. 确定单层递归的逻辑：
单层递归的逻辑就比较好些了 ， 这里我们用重复利用一下t1这个树 ， t1就是合并之后树的根节点（就是修改了原来树的结构） 。
那么单层递归中 ， 就要把两棵树的元素加到一起 。
t1->val += t2->val;接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树 。
t1 的右子树：是 合并 t1右子树 t2右子树之后的右子树 。
最终t1就是合并之后的根节点 。
代码如下：
t1->left = mergeTrees(t1->left, t2->left);t1->right = mergeTrees(t1->right, t2->right);return t1;此时前序遍历 ， 完整代码就写出来了 ， 如下：
class Solution {public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空 ， 合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空 ， 合并之后就应该是t1// 修改了t1的数值和结构t1->val += t2->val;// 中t1->left = mergeTrees(t1->left, t2->left);// 左t1->right = mergeTrees(t1->right, t2->right);// 右return t1;}};那么中序遍历也是可以的 ， 代码如下：
class Solution {public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空 ， 合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空 ， 合并之后就应该是t1// 修改了t1的数值和结构t1->left = mergeTrees(t1->left, t2->left);// 左t1->val += t2->val;// 中t1->right = mergeTrees(t1->right, t2->right);// 右return t1;}};后序遍历依然可以 ， 代码如下：
class Solution {public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空 ， 合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空 ， 合并之后就应该是t1// 修改了t1的数值和结构t1->left = mergeTrees(t1->left, t2->left);// 左t1->right = mergeTrees(t1->right, t2->right);// 右t1->val += t2->val;// 中return t1;}};


推荐阅读


上一篇：方舟私服搭建

下一篇：超实用：MySql+Hibernate实现增删改查0013