江苏龙网

  1. 首页 > 人文 > >

『数学』中考数学备战039-据说这道题90%学生不会做，现在三步带你搞定


『数学』中考数学备战039-据说这道题90%学生不会做，现在三步带你搞定
文章图片
『数学』中考数学备战039-据说这道题90%学生不会做，现在三步带你搞定
文章图片
『数学』中考数学备战039-据说这道题90%学生不会做，现在三步带你搞定
文章图片
这是一道经典的反比例函数难题 ， 据说90%的同学都不能完全做对 。 若是中考出现类似的题目 ， 你能搞定么？如果你相似三角形掌握得不错 ， 第一问可以很快解决 。 但是这个题目的第二问就需要综合运用几个知识 ， 包括相似三角形 ， 反比例函数特殊性质 ， 一组共顶角三角形的面积关系 ， 赶快来学会吧！
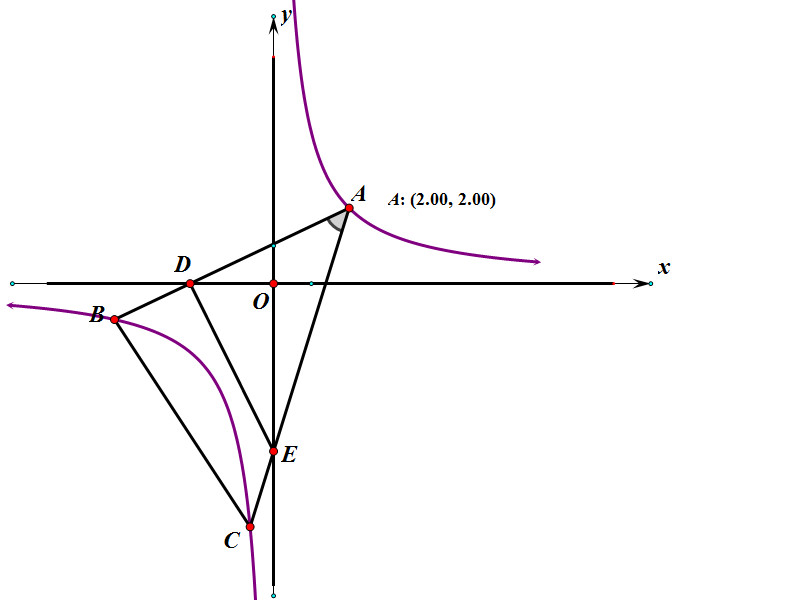
题目：如图 ， A(22)BC均在反比例函数y=(k/x)上 ， ∠BAC=45°.AB交X轴于D ， AC交Y轴于E 。 （1）求S△DOE.    (2)求证：S四边形DBCE=S△ADE
为了便于你很快学会这么题目 ， 我们先把解决此题需要掌握的三个备用知识快速介绍一下 。
备用知识1：相似三角形
1.如图 ， ∠ BAC=45° ， ∠BPC=90°AP平分∠BPC则有△ABP△CAP.
分析：由角BPC=90°∠BAC=45°可知∠ABP+∠ACP=45°.又因为AP平分∠BPC ，
所以∠BPA=∠APC∠ACP+∠CAP=45° ， 可推出∠ABP=∠CAP.所以△ABP△CAP ，
BPPC=(AP^2).
备用知识2:反比例函数的特殊性质 。
如图 ， 直线MN交反比例函数于MN两点 ， 作MA⊥Y轴 ， 作BN⊥X轴 ， 延长AM ， BN交于P则有AB//MNPM/AM=PN/BN.
备用知识3：一组共顶角三角形的面积关系
如图 ， AB分别在三角形CPD的边PC和PD上S△PAB/S△PCD=PAPB/PCPD.
分析与证明：三角形APB的面积=AP×PB×sin∠P
三角形CPD的面积=CP×PD×sin∠P
所以S△PAB/S△PCD=(PAPB)/(PCPD).
学习完了上述三个备用知识 ， 我们就可以快速解决最初的问题了 。
分析与解答：
第一问：直接利用备用知识1的结论 ， 连接AO.DO×EO=AO×AO=8所以S△DOE=4.
第二问：见上图 ， 作AW平行于X轴 ， AH垂直于X轴 ， BW垂直于X轴 ， CH垂直于Y轴 ， DV垂直于AWEK垂直于AH连QGFR.
设QB=aCF=b.
由备用知识2反比例函数的特殊性质可知：
WQ/QB=QG/AG可求WG=(4/a) ， HF/FC=HR/AR可求RH=(4/b) 。
由于GQ//ABAG//QD所以四边形AGQD是平行四边形 ， QD=AG=2
由于RF//AEAR//EF所以四边形AEFR是平行四边形 ， EF=AR=2 。
详细解答过程如下：
【『数学』中考数学备战039-据说这道题90%学生不会做，现在三步带你搞定】
其实很多同学看到这题题目第二问就打算放弃了 ， 但是通过认真学习完完整的解答过程 ， 你会明白难题之所以难 ， 就是同时考查了多个知识点 ， 但其实每一个单独的知识点本身并不难 。 所以打好基础 ， 才是解决难题的最好办法 。


    推荐阅读


    上一篇：「东南大学」东南大学、西南大学、西北大学、东北大学、中南大学最新排位表现

    下一篇：[高职]国家教育部已发布： 高职扩招和 3+2模式专升本啦！