江苏龙网

  1. 首页 > 资讯 > 资讯 > >

面向|“城市计算夏令营”精华课程：面向智慧城市的智能感知技术

“对人和环境泛在、智能感知”是重要的科学前沿研究课题，也是满足智慧城市、公共安全等国家重大需求的关键支撑。为此，《国家创新驱动发展战略纲要》、《国家“十三五”科技创新规划》等将智能感知列为战略任务和重点方向。
城市计算是智慧城市建设的重要支撑，如何大规模、低成本地收集“城市大数据”则是开展城市计算研究的基石。基于静态设施的传统感知技术（典型代表为物联网）存在部署成本高、覆盖范围有限等不足，难以满足城市空间大规模动态感知需求。以群智感知（Crowd Sensing）[1-4]、无线感知（Wireless Sensing）[15-18]等为代表的新型感知技术成为应对公共安全、灾难应急等重大挑战的有效方式，受到国内外学术界和工业界的广泛关注。
群智感知[1-4]利用广泛存在的智能设备（智能手机、可穿戴设备、车载设备等），实现灵活机动且成本低廉的数据收集。移动群智感知(Mobile Crowd Sensing)是群智感知的一种特殊形式，其以大量普通用户及携带的智能设备作为感知节点，利用大众的广泛分布性、灵活移动性和机会连接性实现大规模时空感知。相比群智感知，移动群智感知覆盖范围更广、灵活性更强，是一种“以人为中心”的感知模式，通过利用显式或隐式的大众“智慧”（即群体智能），对低质、冗余、碎片化感知数据进行优选和增强理解，进而为城市计算提供更加优质的数据。移动群智感知关注的主要科学问题是：1）如何合理选择和协同泛在、互补的群体感知能力实现高质量感知；2）如何高效处理和融合低质、冗余的群体感知数据实现准确理解。
无线感知的基本原理是：环境中传播的无线信号, 会由于感知目标（人或物）的存在而产生反射、衍射、散射等现象，使得接收设备所接收信号（即回波信号）的振幅、相位等特征发生变化，通过检测和分析信号的变化特征，便可推断感知目标的位置、状态等信息，达成感知之目的。相较于图像感知、可穿戴感知等技术，基于普通商用设备的无线感知不需在环境中部署任何专用传感设备，也不需感知目标携带任何传感器，具有普适程度高、感知范围广、感知成本低、不侵扰用户、不泄露隐私等特点和优势，是实现城市感知的理想形式，具有广阔的应用前景。无线感知关注的主要科学问题是：1）无线感知的理论模型和一般机理，揭示感知极限；2）无线感知的精准性和鲁棒性，降低环境改变、个体差异等对性能的影响。
针对城市感知需求和上述科学问题，西北工业大学人机物融合智能计算团队在国家自然科学基金、国家“973计划”等科研项目的支持下，在国际上较早开展并持续深入开拓移动群智感知、智能无线感知相关理论与方法研究，取得系列创新成果。
一、移动群智感知
结合移动群智感知关键科学问题，重点在感知任务分配、感知数据汇聚、群智融合计算等方面开展研究工作。
1.感知任务分配
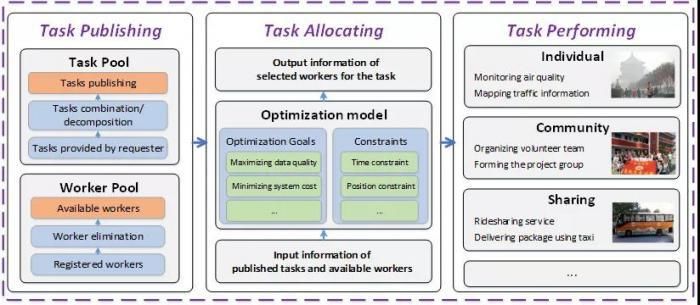
移动群智感知任务分配涉及两类重要实体，即感知任务和任务参与者，关键在于如何利用优化模型和算法，在候选者集合中选择优质的参与者执行任务，以保证低成本地获取足量的优质数据。任务分配通用模型如图1所示。
面向|“城市计算夏令营”精华课程：面向智慧城市的智能感知技术
文章图片

▲图1 任务分配模型
1.1 面向单任务的参与者选择
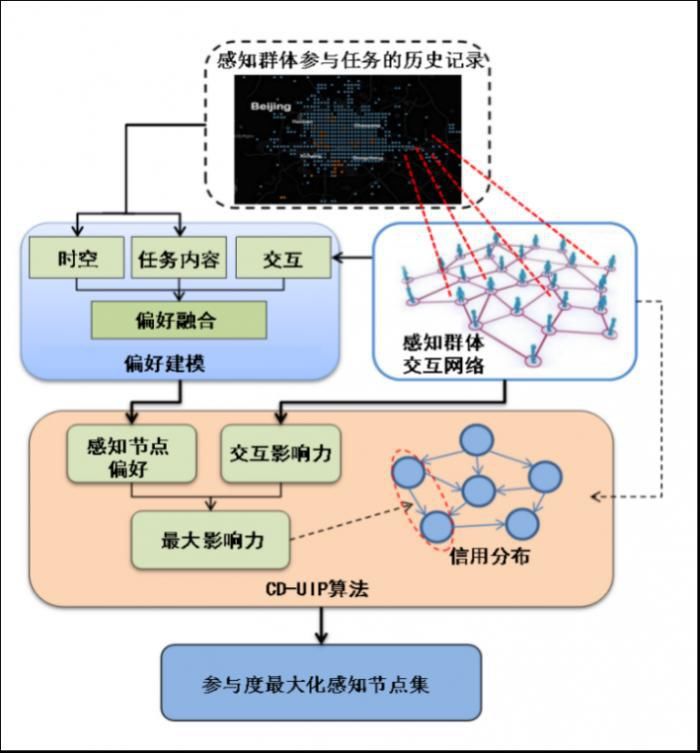
针对如何为城市空间中的单个感知任务（如城市某重点区域交通动态）选择合适感知节点这一问题，提出了基于信用分布的影响力最大化算法，预测感知参与度。将基于事件的社交网络（EBSN, Event-Based Social Network）的活动视为感知任务，综合考虑任务的内容特征、时空情境特征和社会影响特征，提高预测用户参与任务的准确率，即提高感知能力发现和任务分配的命中率。如图2所示，将感知节点挑选的问题形式化为偏好-影响力集合选择问题，即寻找对当前感兴趣且具有影响力的用户集。方法框架包括用户-任务偏好建模和影响力最大化两个部分。相关工作发表在ACM UbiComp 2015[5]。
面向|“城市计算夏令营”精华课程：面向智慧城市的智能感知技术
文章图片

▲图2 基于信用分布的感知任务参与影响力最大化算法
1.2 面向多任务的参与者选择
1.2.1同构多任务分配
移动群智感知任务往往并发出现，其中感知节点数量与任务数量的比例影响了感知能力优化组合的方式，主要存在两种情况：感知节点资源充足和感知节点资源匮乏。
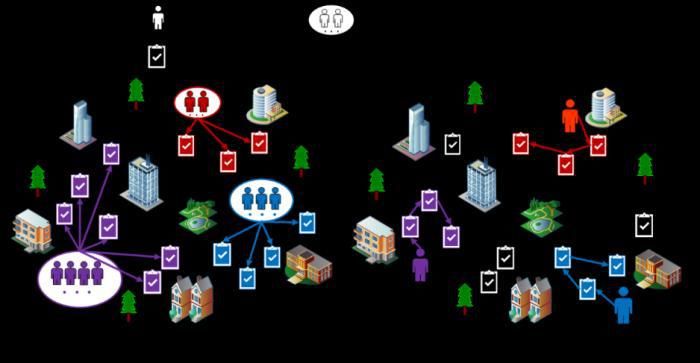
针对感知节点资源充足的情况，要求每个工作者完成一个任务以保证任务完成的质量，优化目标是最小化移动距离和激励成本。针对该问题，利用多目标优化模型求解，分别通过线性加权法和妥协约束法将双目标转化为单目标，采用整数线性规划方法（如分支定界法）求解。
面向|“城市计算夏令营”精华课程：面向智慧城市的智能感知技术
文章图片

（1）感知节点资源充足 （2）感知节点资源匮乏
▲图3 面向多任务的感知能力优化组合
针对感知节点资源匮乏情况，需要每个工作者完成多个任务以增加任务被完成的总比例（即任务完成率）。此时，优化的目标是最大化个体任务分配个数以提高任务完成率和最小化群体移动距离以缩短任务完成时间。针对该问题，利用最小费用最大流模型，提出基于增广链（Augment Path）的优化算法，其中费用代表移动距离，流代表完成的任务个数；根据优化目标，为工作者分配最短移动距离的任务集且保证每个任务得到尽可能充足的工作者。相关研究成果发表于顶级国际会议ACM UbiComp 2016[6]。


推荐阅读


上一篇：王漫妮|余文乐祝福王漫妮看来三十而已真的是火出圈了

下一篇：改姓|贝索斯前妻改姓新的姓氏来自她的祖父