д»ҺBengioжј”и®ІеҸ‘ж•ЈејҖжқҘпјҡжҺўи®ЁйҖ»иҫ‘жҺЁзҗҶдёҺжңәеҷЁеӯҰд№ ( е…« )
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еӣҫ 1. MAXSAT еұӮзҡ„еүҚеҗ‘дј йҖ’ гҖӮ иҜҘеұӮе°Ҷе·ІзҹҘ MAXSAT еҸҳйҮҸзҡ„зҰ»ж•ЈжҲ–жҰӮзҺҮиөӢеҖјдҪңдёәиҫ“е…Ҙ пјҢ йҖҡиҝҮжқғйҮҚ S зҡ„ MAXSAT SDP жқҫејӣиҫ“еҮәеҜ№жңӘзҹҘеҸҳйҮҸиөӢеҖјзҡ„зҢңжөӢ гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖҗеұӮеҲқе§ӢеҢ–гҖ‘
еҲқе§ӢеҢ– SATNet ж—¶ пјҢ з”ЁжҲ·еҝ…йЎ»жҢҮе®ҡиҜҘеұӮеҸҜд»ҘиЎЁзӨәзҡ„жңҖеӨ§еӯҗеҸҘж•° m гҖӮ йҖҡеёёеёҢжңӣе°Ҷ m зҡ„еҖји®ҫзҪ®зҡ„иҫғдҪҺ пјҢ еӣ дёәдҪҺ秩结жһ„еҸҜд»ҘйҳІжӯўеҮәзҺ°иҝҮжӢҹеҗҲзҡ„й—®йўҳ пјҢ д»ҺиҖҢжҸҗй«ҳжіӣеҢ–иғҪеҠӣ гҖӮ иҖғиҷ‘еҲ°иҝҷз§ҚдҪҺ秩结жһ„ пјҢ з”ЁжҲ·еёҢжңӣйҖҡиҝҮиҫ…еҠ©еҸҳйҮҸеңЁдёҖе®ҡзЁӢеәҰдёҠжҸҗй«ҳеұӮзҡ„иЎЁзӨәиғҪеҠӣ гҖӮ иҝҷйҮҢзҡ„й«ҳзә§зӣҙи§үжқҘиҮӘдәҺеёғе°”ж»Ўи¶ій—®йўҳзҡ„еҗҲеҸ–иҢғејҸпјҲConjunctive Normal Form пјҢ CNFпјүиЎЁзӨә гҖӮ еҗ‘й—®йўҳдёӯж·»еҠ йўқеӨ–зҡ„еҸҳйҮҸеҸҜд»Ҙжҳҫи‘—еҮҸе°‘жҸҸиҝ°иҜҘй—®йўҳжүҖйңҖзҡ„ CNF еӯҗеҸҘзҡ„ж•°йҮҸ гҖӮ
жңҖеҗҺ пјҢ д»Ө k=sqrt(2n)+1 пјҢ n йҷӨдәҶиҫ…еҠ©еҸҳйҮҸеӨ–иҝҳжҚ•иҺ·е®һйҷ…й—®йўҳеҸҳйҮҸзҡ„ж•°йҮҸ гҖӮ иҝҷд№ҹжҳҜжң¬ж–Үзҡ„ MAXSAT жқҫејӣе…¬ејҸпјҲ2пјүжҒўеӨҚе…¶зӣёе…і SDP зҡ„жңҖдјҳи§ЈжүҖйңҖзҡ„жңҖе°Ҹ k еҖј гҖӮ
гҖҗж”ҫжқҫеұӮиҫ“е…ҘгҖ‘
йҰ–е…Ҳе°Ҷе…¶иҫ“е…Ҙ Z_I жқҫејӣжҲҗиҝһз»ӯеҗ‘йҮҸз”ЁдәҺ SDP е…¬ејҸпјҲ2пјү гҖӮ д№ҹе°ұжҳҜиҜҙ пјҢ е°ҶжҜҸдёҖеұӮиҫ“е…Ҙ z_l пјҢ lвҲҲI жқҫејӣеҲ°дёҖдёӘзӣёе…ізҡ„йҡҸжңәеҚ•дҪҚеҗ‘йҮҸ z_l пјҢ v_lвҲҲR^kпјҡ
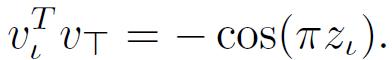 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҲ4пјү
е…¬ејҸпјҲ4пјүж»Ўи¶іпјҡ
пјҲ5пјү
е…¶дёӯ пјҢ (v_l)^rand дёәйҡҸжңәеҚ•дҪҚеҗ‘йҮҸ гҖӮ
гҖҗйҖҡиҝҮ SDP дә§з”ҹиҝһз»ӯзҡ„иҫ“еҮәжқҫејӣгҖ‘
з»ҷе®ҡиҝһз»ӯиҫ“е…Ҙжқҫејӣ V_I пјҢ дҪҝз”Ёеқҗж ҮдёӢйҷҚжӣҙж–°е…¬ејҸпјҲ3пјүжқҘи®Ўз®—иҝһз»ӯиҫ“еҮәжқҫејӣ v_o гҖӮ еҖјеҫ—жіЁж„Ҹзҡ„жҳҜ пјҢ еқҗж ҮдёӢйҷҚжӣҙж–°еҸӘи®Ўз®—иҫ“еҮәеҸҳйҮҸ пјҢ д№ҹе°ұжҳҜиҜҙ пјҢ дёҚи®Ўз®—е…¶иөӢеҖјдҪңдёәеұӮиҫ“е…Ҙзҡ„еҸҳйҮҸ гҖӮ
еүҚеҗ‘дј йҖ’зҡ„еқҗж ҮдёӢйҷҚз®—жі•иҜҰз»ҶиҜҙжҳҺеңЁз®—жі• 2 дёӯ гҖӮ иҜҘз®—жі•дҝқз•ҷдәҶи®Ўз®— g_o жүҖйңҖзҡ„О©=VS^T йЎ№ пјҢ 然еҗҺеңЁжҜҸж¬ЎеҶ…йғЁиҝӯд»ЈдёӯйҖҡиҝҮ秩 1 жӣҙж–°еҜ№е…¶иҝӣиЎҢдҝ®ж”№ гҖӮ еӣ жӯӨ пјҢ жҜҸж¬Ўиҝӯд»Јзҡ„иҝҗиЎҢж—¶й—ҙжҳҜ O(nmk) гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖҗз”ҹжҲҗзҰ»ж•ЈжҲ–жҰӮзҺҮиҫ“еҮәгҖ‘
з»ҷе®ҡеқҗж ҮдёӢйҷҚзҡ„жқҫејӣиҫ“еҮә V_O пјҢ еұӮйҖҡиҝҮйҳҲеҖјжҲ–йҡҸжңәеҸ–ж•ҙе°Ҷиҝҷдәӣиҫ“еҮәиҪ¬жҚўдёәзҰ»ж•ЈжҲ–жҰӮзҺҮеҸҳйҮҸиөӢеҖј Z_O гҖӮ йҡҸжңәеҢ–иҲҚе…Ҙзҡ„дё»иҰҒжҖқжғіжҳҜ пјҢ еҜ№дәҺжҜҸдёҖдёӘ v_o пјҢ oвҲҲO пјҢ еҸҜд»Ҙд»ҺеҚ•дҪҚзҗғйқўдёҠеҸ–дёҖдёӘйҡҸжңәи¶…е№ійқў r 并иөӢеҖј гҖӮ
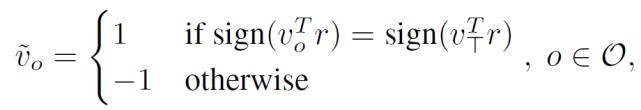 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҲ6пјү
з»ҷе®ҡжӯЈзЎ®зҡ„жқғеҖј пјҢ иҝҷз§ҚйҡҸжңәеҸ–ж•ҙиҝҮзЁӢдҝқиҜҒдәҶжҹҗдәӣ NP-hard й—®йўҳзҡ„жңҖдҪіжңҹжңӣйҖјиҝ‘жҜ” гҖӮ еңЁи®ӯз»ғжңҹй—ҙ пјҢ жІЎжңүжҳҺзЎ®ең°жү§иЎҢйҡҸжңәеҸ–ж•ҙ гҖӮ зӣёеҸҚ пјҢ v_o е’Ң v_T еңЁз»ҷе®ҡ r зҡ„еҗҢдёҖдҫ§зҡ„жҰӮзҺҮжҳҜпјҡ
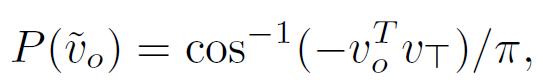 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҲ7пјү
еңЁжөӢиҜ•иҝҮзЁӢдёӯ пјҢ ж—ўеҸҜд»Ҙд»ҘзӣёеҗҢзҡ„ж–№ејҸиҫ“еҮәжҰӮзҺҮиҫ“еҮә пјҢ д№ҹеҸҜд»ҘйҖҡиҝҮйҳҲеҖјеҲҶеүІжҲ–йҡҸжңәиҲҚе…Ҙиҫ“еҮәзҰ»ж•ЈиөӢеҖј гҖӮ еҰӮжһңдҪҝз”ЁйҡҸжңәеҢ–иҲҚе…Ҙ пјҢ еҲҷжү§иЎҢеӨҡж¬ЎиҲҚе…ҘеҗҺе°Ҷ z_o и®ҫдёәдҪҝе…¬ејҸпјҲ1пјүдёӯ MAXSAT зӣ®ж ҮжңҖеӨ§еҢ–зҡ„еёғе°”и§Ј гҖӮ
жңҖеҗҺ пјҢ дҪңиҖ…и®Ёи®әдәҶеҗҺеҗ‘дј йҖ’ пјҢ еҚі пјҢ йҖҡиҝҮ SATNet layer иҺ·еҫ—еҸҚеҗ‘дј ж’ӯжӣҙж–° пјҢ дҪҝе…¶иғҪеӨҹйӣҶжҲҗеҲ°зҘһз»ҸзҪ‘з»ңдёӯ гҖӮ еҹәдәҺеұӮиҫ“еҮәз»ҷе®ҡзҪ‘з»ңжҚҹеӨұ l зҡ„жўҜеәҰОҙl/ОҙZ_O пјҢ ж №жҚ®еұӮиҫ“е…Ҙе’ҢжҜҸеұӮжқғйҮҚОҙl/ОҙS и®Ўз®—жўҜеәҰОҙl/ОҙZ_I гҖӮ з”ұдәҺжҳҫејҸеұ•ејҖеүҚеҗ‘дј йҖ’计算并еӯҳеӮЁдёӯй—ҙ Jacobians еңЁж—¶й—ҙе’ҢеҶ…еӯҳж–№йқўж•ҲзҺҮдҪҺдёӢ пјҢ еӣ жӯӨдҪңиҖ…йҮҮз”ЁдәҶй«ҳж•Ҳзҡ„еқҗж ҮдёӢйҷҚз®—жі•жҺЁеҜјеҮәзӣҙжҺҘи®Ўз®—жңҹжңӣжўҜеәҰзҡ„и§ЈжһҗиЎЁиҫҫејҸ гҖӮ з®—жі• 1 жҖ»з»“дәҶи®Ўз®—иҝҷдәӣжўҜеәҰи®Ўз®—зҡ„жӯҘйӘӨ гҖӮ
гҖҗд»ҺжҰӮзҺҮиҫ“еҮәеҲ°иҝһз»ӯжқҫејӣгҖ‘
з»ҷе®ҡ Оҙl/ОҙZ_O пјҢ еҸҜд»ҘйҖҡиҝҮжҰӮзҺҮеҲҶй…ҚжңәеҲ¶жҺЁеҜјеҮә Оҙl/ОҙV_Oпјҡ
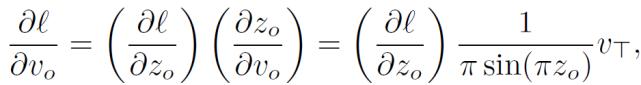 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жҺЁиҚҗйҳ…иҜ»
- AMDCESеҸ‘еёғдјҡ1жңҲ13ж—ҘеҮҢжҷЁ0зӮ№ејҖе§ӢпјҡиӢҸе§ҝдё°дҪңдё»йўҳжј”и®І
- AMDе®ҳе®ЈCEOиӢҸе§ҝдё°CESжј”и®Іпјҡй”җйҫҷ5000笔记жң¬жү“еӨҙйҳө
- йӮ¬иҙәй“ЁйҷўеЈ«жј”и®ІжқғеЁҒеҸ‘еёғпјҡ 5Gе•Ҷз”ЁдёҖе‘Ёе№ҙ дә§дёҡеҲӣж–°еҶҚеҮәеҸ‘
- 马дә‘жңҖж–°жј”и®ІпјҡиҝҮеәҰејәи°ғз®ЎзҗҶпјҢе°ұеҚҮзә§жҲҗз®ЎжҺ§пјҢжңҖеҗҺжҲҗдёәжҺ§еҲ¶
- NVIDIA GTC 2020з§ӢеӯЈз«ҷдё»йўҳжј”и®Ідёӯж–Үеӯ—幕зүҲдёҠзәҝ
- 2020дё–з•ҢVRдә§дёҡеӨ§дјҡдә‘еі°дјҡжј”и®Іеҳүе®ҫ | 2018е№ҙеӣҫзҒөеҘ–иҺ·еҫ—иҖ…пјҢи’ҷзү№еҲ©е°”еӨ§еӯҰж•ҷжҺҲYoshua Bengio
- жҷәз”өзҪ‘|MIDCејҖ幕 йӣ·еҶӣжј”и®ІпјҢ第еӣӣеұҠе°ҸзұіејҖеҸ‘иҖ…еӨ§дјҡ
- еҚ—ж–№PLUS|вҖңдәәжүҚж—ҘвҖқжј”и®Іеҳүе®ҫйҷҲе®ҒпјҡAIвҖңиҝҪе…үиҖ…вҖқзҡ„жё©жҡ–ең°еёҰ
- зҲұеӣ е„ҝ科жҠҖ|并жҸҗеҮәи§ЈеҶіж–№жЎҲпјҢеҗҙжҒ©иҫҫжј”и®ІзӣҙжҢҮAIиҗҪең°дёүеӨ§жҢ‘жҲҳ
- 科жҠҖеЈ№йӣ¶жү’|BengioгҖҒжқЁејәгҖҒе”җеү‘йўҶиЎ”пјҒжҺўи®ЁеҰӮдҪ•жһ„е»әAIеӯҰжңҜз ”з©¶е’Ңдә§дёҡиҗҪең°зҡ„жЎҘжўҒ














