微积分▲微积分思维，是对传统降维方法的一次打击。简单点也不难！微积分

文章图片

文章图片

文章图片
在工程设计中，普遍地会用到微积分来分析曲面实体的体量大小或内力分布。所以学设计的，总要掌握一些微积分的知识才好。
在学习微积分之初，老师经常会引用恩格斯在《自然辩证法》中对微积分的一句评价：

只有微积分才能使自然科学有可能用数学来不仅仅表明状态，并且也表明过程：运动。

从字面的表达看， “状态”有静态的含义。比如平面坐标系内X轴上的一个点，我们这样来表明它的状态：（x1 ， 0）。点的维度是0 。让这个点沿X轴运动，在运动到坐标（x2 ， 0）时，我们这样来表明它的过程：x2-x1 。这是一条直线，直线是一维的。
以此类推，还可以进阶到二维的面，三维的体，四维以至N维。
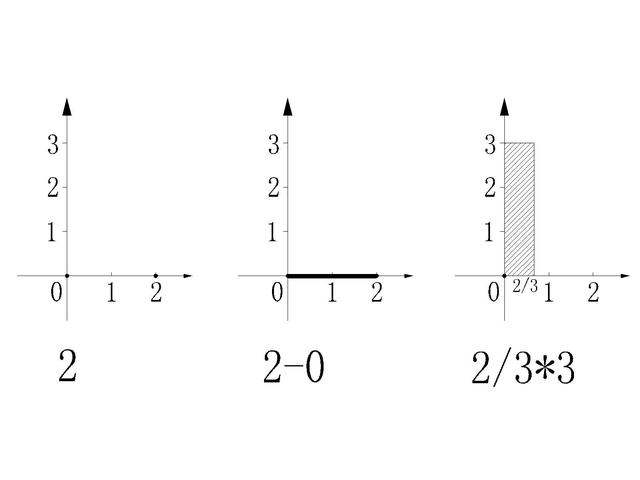
我们以一个自然数2为例，做两个简单的变换，得出两个等式：2=2-0和2=2/3*3 。
正在辅导孩子小学数学的孩儿他妈看到此处，当即暴起，表示这是脱了裤子放屁！
好吧，我们看图说话：
看似简单无脑的变换式，让我们实现了从低维到高维的思维过渡。
通过上述的两个等式，又得到一个新的等式：2/3*3=2-0 。我们可以这样理解它的含义：

一个二维的正方形的面积可以与一条一维的直线段的长度等值。这种等值关系，就是两个维度空间的通道。

把上面的几个等式先放一边，我们来求一个曲线三角形的面积。
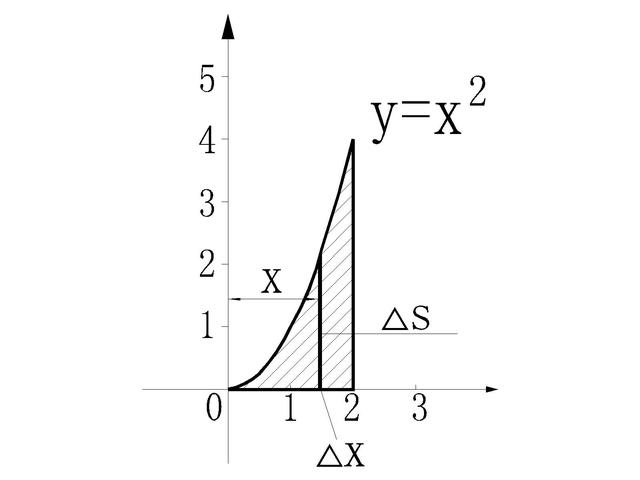
如上图，曲线三角形的斜边是曲线y=x^2的一部分，对应的x∈[0 ， 2
，求阴影部分也就是曲线三角形的面积。
首先，我们在X轴上取值x ，使0≤x≤2 。再取一个无限小的增量Δx ，这个增量Δx ，小到多小呢？小到可以忽略不计，所以有（x+Δx）^2无限约等于x^2 。
这样，我们就得到一个无限近似的长方形， X轴向的边长为Δx ， Y轴向的边长为x^2 ，
它的面积：ΔS=x^2*Δx 。
从形式表达的结果看， ΔS也是一个无限小的量。
而在x∈[0 ， 2
上，有无限个ΔS ，它们的累加结果，就是曲线三角形的面积S 。
我们用一个积分等式，来表达上述的结果：
这个等式本身是无法解的。
但从等式2/3*3=2-0中，我们得到过这个启示：

一个二维的正方形的面积可以与一条一维的直线段的长度等值。

那么，我们就去找出与这个曲线三角形等值的直线来。
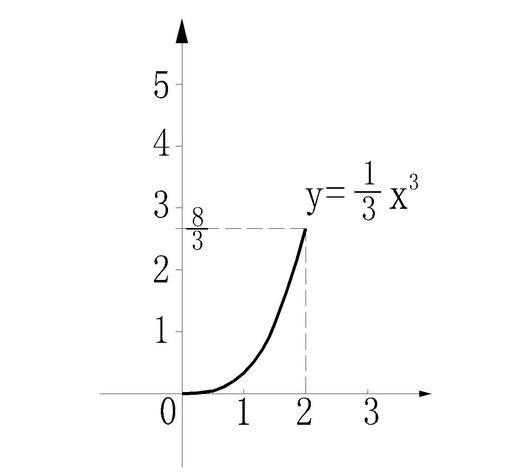
下图是曲线y=1/3 x^3的一部分，对应的x∈[0 ， 2
。
当x∈[0 ， 2
时， y∈[0 ， 8/3
。
这个很好计算。取x1=0 ，则y1=1/3*0^3=0；取x2=2 ，则y2=1/3*2^3=8/3；
那么，两个端点在Y轴的投影距离y2-y1=8/3-0=8/3 。
这条直线，就是我们要找的直线。接下来的工作，就是证明曲线三角形的面积与这条直线的长度等值，即：
S= ∫x^2*dx ， x∈[0 ， 2
=y2-y1
首先，我们在这条直线上，也取一个无限小的量Δy 。
在x∈[0 ， 2