江苏龙网

  1. 首页 > 资讯 > 资讯 > >

|想要看懂《信条》，演反间时懂先得你( 二 )


|想要看懂《信条》，演反间时懂先得你
本文图片

我们可以看到 ， 系统的熵在可逆绝热过程中不变 ， 在不可逆绝热过程中增加 。 这就是著名的熵增加原理 。 它还可以表述为：孤立系的熵永不减少 。 孤立系指的是绝热、且没有外界做功的系统 。 但是这并不意味着系统的熵永不减少 ， 如果不加上绝热或者孤立的条件 ， 比如挨了一顿批以后的你做功把房间整理好 ， 那么房间的熵也会减少 。
在1870年 ， 波尔兹曼通过分析体系中微观组分的统计行为、发展了熵在统计学上的定义 。 与此相关的一个著名关系式是波尔兹曼关系（值得一提的是 ， 这个表达形式是由普朗克得出 ， 而非波尔兹曼本人）
K是波尔兹曼常数 ， W是某个分布对应的系统量子态数 。 这个关系式将热力学几率和熵联系起来 ， 并给出我们所熟知的熵的统计解释：熵代表体系的混乱度（或无序度）;热力学几率越大 ， 也即相应的微观状态数越多 ， 代表系统越混乱 。
03
时间反演
说到时间反演 ， 常常被提到的一个例子就是电影的倒放 ， 就好像《信条》预告片中射出的子弹以相反的动量沿着原轨迹回到枪膛 。
|想要看懂《信条》，演反间时懂先得你
本文图片

在经典力学的框架下 ， 保守力场中的时间反演——或者说运动的逆转——是可实现的 。 假设一个粒子在保守力场中沿着一条确定的轨迹运动 ， 运动方程为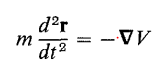
|想要看懂《信条》，演反间时懂先得你
本文图片

假设r1(0)和p1(0)是粒子在时刻t=0的位置和所具备的动量 ， 我们在相同的时刻让初始条件为r2(0)=r1(0)和p2(0)=-p1(0)的相同粒子开始运动 ， 可以看到 ， 运动方程允许这个粒子沿着前一个粒子的轨迹逆向运动 ， 在t=t2时刻 ， 第二个粒子回到了第一个粒子在t=-t2时刻所处的位置 ， 但是二者的动量方向是相反的 。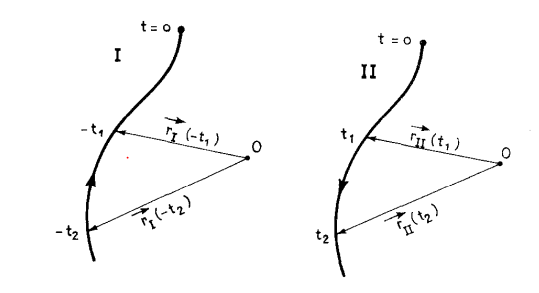
|想要看懂《信条》，演反间时懂先得你
本文图片

来源：参考文献[3]
这也就是说 ， 如果在时间逆转（t→-t）的情况下 ， 粒子所遵循的运动方程（量子力学框架下则是薛定谔方程）仍旧成立 ， 那么时间反演在理论上似乎是可行的 。 但实际生活中我们并不能看到跌落破碎的鸡蛋凌空升起在桌上复原、也无法看到爆炸的碎片沿着原来的路径返回而重新组装成一栋大厦 ， 这都是因为热力学第二定律中的熵增加原理 ， 使得宏观的时间反演无法实现 。
|想要看懂《信条》，演反间时懂先得你
本文图片

04
轻剧透预警
不同以往的科幻电影中 ， 主角们往往乘坐一个时空机器回到过去 ， 然后时间继续正向流动；诺兰创造了一个“门” ， 穿过门后 ， 时间箭头掉转 ， 世界沿着熵减的方向发展 。
|想要看懂《信条》，演反间时懂先得你
本文图片

主角们看到消防车喷出的水流回水管 ， 救援人员倒着走离开现场 ， 想要捡起一块未来的子弹 ， 不能伸手去抓 ， 而是要做出丢弃的动作 。
|想要看懂《信条》，演反间时懂先得你
本文图片

从某种意义上讲 ， 《信条》的这个设定相对来说更为科学——就像粒子必须沿着相同的路径运动同样的时间才能回到最初的起点 ， 穿过时间“门” ， 你无法直接回到一天前 ， 而是要沿着时间河流往回走上一天 ， 告诉过去那个自己：看在个点条头的所理物天明给 。 而在这个过程中 ， 你看到的一切都是倒映的 ， 逆向经历了这一天的你知道了这一天将要发生什么 ， 当你获得了所有信息以后 ， 就可以再次通过“门” ， 回到正向的时间 ， 迅速调整自己的安排 ， 确保在文章发出的第一时间打开公众号、点个在看 。 而明白这一点 ， 就能明白诺兰在“时间”上做的手脚了 。
|想要看懂《信条》，演反间时懂先得你
本文图片

看到这里 ， 屏幕前的各位朋友想必和小编一样 ， 露出了三分薄凉 ， 三分嘲讽和四分漫不经心的微笑：不就是时间逆转吗 ， 我已洞悉其中奥妙 ， 《信条》对我来说根本就不算个事儿
|想要看懂《信条》，演反间时懂先得你
本文图片


推荐阅读


上一篇：天文|我们似乎总是更爱假设外星人拥有比我们更加先进的科技

下一篇：暖心 大学|“暖心公主抱”女生考上大学 拿着录取通知书与民警分享喜悦