数学|后浪变前浪,一定会被拍死在沙滩上吗?未必……( 二 )
一个合格的“后浪”:
KdV 方程的孤波解
让我们把故事线跳转到1834年的夏天 。
话说 , 在英国爱丁堡格拉斯哥的运河旁 , 苏格兰工程师罗素(John Scott Russell)正骑马漫步 。 突然间 , 运河中一个奇怪的波浪引起了他的注意[2] 。
根据他事后的描述[3, 4] , 运河上的船“突然停下来??大量河水并不停止 , 它们汇集在船头附近??形成一个圆而光滑、轮廓分明、巨大的孤立的高水头 , 沿着运河继续前进 , 没有明显的形状改变和速度减小 。 ”
约翰·罗素(左)vs伯特兰·罗素(右) | Wikipedia
约翰·罗素是苏格兰海军工程师 , 也就是上面奇怪波浪的发现者 , 同时还是1851年世博会的发起人 。
然而大家一般提起“罗素” , 往往指的是《西方哲学史》的作者 , 提出了“罗素悖论”的伯特兰·罗素 。 然而他与今天的故事——毫无关系??
(这里放上伯特兰·罗素的照片纯粹就是为了防止有的同学认错人 。 )
考虑到奇怪波浪的形状和移动速度都保持不变 , 罗素首先用“solitary”来形容这一类波 , 即孤波(solitary wave) 。
为了弄清楚孤波的形成原因 , 罗素建造了一个一端带有重锥的水槽 , 用重锤落入水槽的一端来产生孤波 。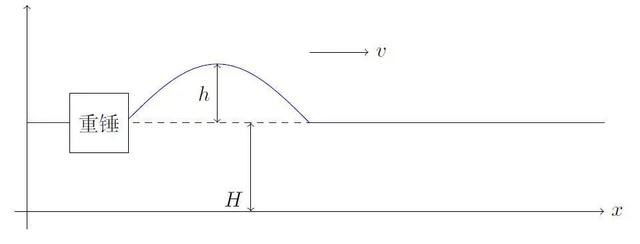
罗素实验示意图
重锤落水后 , 产生的孤波以恒定的速度v向右移动并保持形状不变 。
在实验中 , 罗素还发现水槽的静水水深H与孤波的振幅h有如下关系: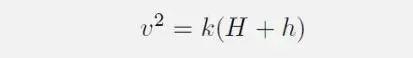
其中k是比例常数 。 这说明振幅较高的孤波移动速度也更快 。 此外 , 实验证明孤波中水的体积相当于重锤排开的水的体积 , 所以振幅高的波也相对较窄 。
不过可惜的是 , 罗素并没有尝试从流体力学的角度分析这个问题 , 也没有给出孤波的数学解释[3, 4] , 所以在接近半个世纪的时间里 , 他的研究始终没有受到重视 。
直到1895年 , 荷兰数学家科特韦格(Diederik Korteweg)和德弗里斯(Gustav de Vries)提出了KdV方程 , 才从数学上肯定了罗素当年的发现 。
布辛尼斯克(左)、科特韦格(中)、德弗里斯(右)| Wikipedia
布辛涅斯克 , 法国数学家 。 布辛尼斯克在其1877年的著作[5]中已经得出相关的结论 。 不过直到1895年科特韦格与他的学生德弗里斯发表了他们关于浅水中小振幅长波运动的方程之后[6] , 相关研究才逐渐在学术界得到重视 , 所以最终也以两人的名字将方程命名为KdV方程 。
KdV方程最初写作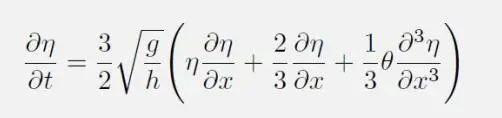
通过变量替换进行简化处理(即无量纲化)后得到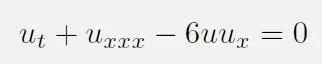
关于KdV方程的推导 , 过程稍显冗长 , 感兴趣的读者可以参考[2,7] 。 (事实上笔者确信已找到了一种绝妙的推导方法 , 可惜这里空白的地方太小 , 写不下……)
这里的无量纲化 , 指的是通过合适的变量替换 , 将方程中涉及物理量的部分的单位移除 , 总之是一种简化运算的手段 。
求解KdV方程的思路有很多 , 经典的包括行波法、Lax对法、双线性算法、反散射方法等等 , 这些思路也是现代可积系统研究的主要方向 。 这里简要介绍行波解的求法 。
不失一般性 , 我们讨论无量纲化的KdV方程
假设方程存在以下形式的解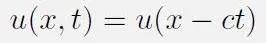
将其带入KdV方程 , 稍作处理就可以得到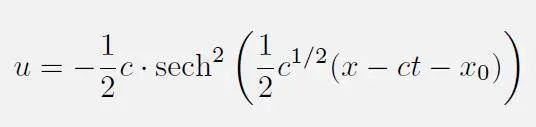
其中符号的含义与上文相同 , c为波速 , x0为任意常数 。
这样我们就得到了一个合格的“后浪”:局域分布(只存在于空间中的一个小区域) , 且形状不随时间演化 。
之后我们还会看到 , 孤波间作用后还具有弹性碰撞的性质(即碰撞后 , 形状能够恢复 , 且没有动能损失) 。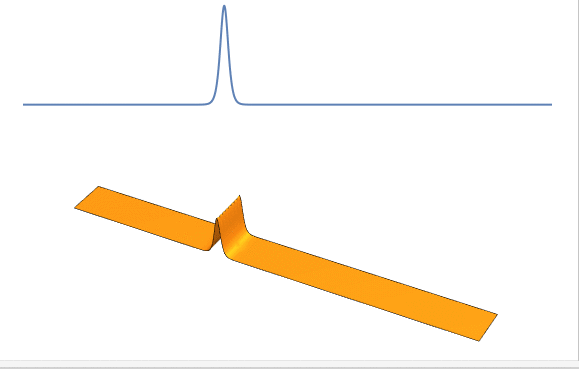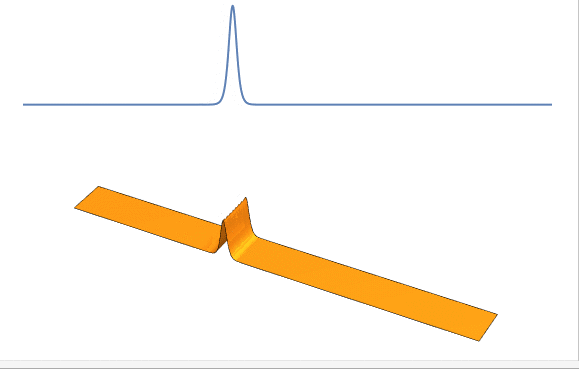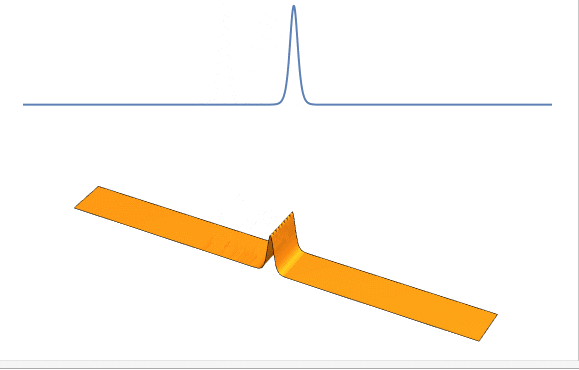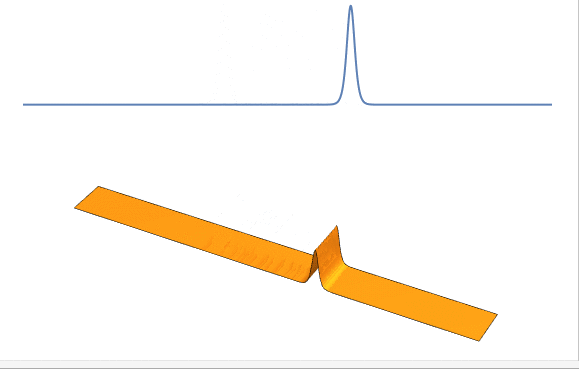
KdV方程的孤波解 | 作者绘制
孤波形成的数学原理:
挤压与色散
现在 , 我们回过头来思考孤波形成的数学原理 。
推荐阅读
- 天文|太空中的数学美感,银河系中已知最大的气态结构
- 全视角|《后浪》为何遭青年们的指责?前浪不欠你们什么,奋斗是你们的事
- 旅游那点事|王宝强没文化?刘昊然爆料:我高考数学是宝强哥帮忙温习的
- 消息资讯|泉商“后浪”劲霸洪锽淮、九牧林晓伟上榜胡润创业领袖
- 学子|sat2数学详情介绍
- 运算|厦门事业单位行测数量关系技巧:数学运算作答策略
- 教学|邵东市小学数学教师“提升教学反思能力”专题研讨会圆满结束
- 教学|中山这些家长走进开放课堂,上语文数学航模陶艺管乐课……
- 物理|后浪!50席”国字号“物理学霸,湖南选手拿下20席
- 考试|4563数学问 2020年普通高等学校招生全国统一考试理科数学二卷原题和答案



















