数学|数学之美!数学家的这些兴奋点,你能理解吗?
在学习和日常生活中 , 不少人认为数学是理性的、枯燥的 。 但其实数学是纯粹的 。 它不需要华丽的修饰 , 一道道简洁又从容的公式 , 就能表达出这种纯粹的逻辑之美 。 素数出现在我们的生活中 , 又体现在生物进化的历程中 , 更让无数的数学家为之呕心沥血、如痴如醉 。
出品:"格致论道讲坛"公众号(ID:SELFtalks)
以下内容为中国科学院数学研究所博士生导师、研究员徐晓平演讲实录:
一提到数学 , 一般人都觉得太枯燥无味 。 但细细想、细细看 , 它又无处不在 。 今天我们从逻辑的角度 , 来领略数学的美 。
首先 , 什么是数学?它是科学的描述和研究事物规律的方法和工具 , 是人类逻辑思维文明的重要体现 , 更是逻辑思维文明的发展平台 。
我曾经问一个法国教授 , 数学有什么用?他告诉我 , 数学能使人更聪明 , 数学的价值不能单靠物质上是否有用来衡量 。 美国华尔街的金融机构 , 雇佣了大量的数学博士 , 看重的就是他们逻辑思维能力 。
素数之美
自然数1、2、3、4、5 , 出现在古代人类文明中有五千年以上的历史 。 可是人们对自然数的认识 , 却是一个漫长发展的过程 。 比如说素数 , 也称为质数 , 是大于1的整数 , 它不能写成小于它的两个正整数之积 , 例如素数2、3、5、7、11、13、17、19等 。
素数最早出现在古代埃及分数中 。 有5张大饼平均分给8个人 , 怎么分?先看古埃及怎么分 , 将其中4张各切成两半 , 剩下张切成8块 , 每个人的份额是半块加1/8块 。
用现代数学表示 , 就是5/8等于1/2加1/8 , 它就是一个埃及素数 。 它是古埃及人刺在一种不易腐烂的树叶上的分配方案 , 是考古学家发现的 。 如果一个数是有限个分子为一的分数之和 , 它被称为埃及分数 。 古埃及人在类似的分配方案中 , 意识到了素数的特性 。
对素数的研究的记载 , 最早出现在公元前300年的古希腊人欧几里得的《几何原本》中 。 欧几里得证明了有无穷多个素数 , 那么有没有更好的数素数方法呢?有 , 这就是所谓的素数定理 。
我们数数看 , 小于X的正整数里有多少个素数?X小的时候能数 , X大了很难数了 。 而素数定理告诉你 , 当X充分大的时候 , 这个值与X除于LnX的值相近 。 近看小于x的素数值看不出所以然来 , 远看它却表现出优美的规律 , X除以lnX , 这就是数学的美妙之处 。
这是18世纪末 , 由高斯和勒让德独立发现的 , 但是并不是由他们证明 。 他们的发现只是一种猜测 。 两个人试图证明过 , 但没有成功 。 后来Chebyshev在1851年 , Riemann在1859年尝试过并取得了进展 , 但是还是没有完全解决问题 。
最终 , 1896年 , Hadamard和Poussin独立地完成了证明 。 也许你会问素数有什么用?动物学家发现某些蝉的演化用到了素数 。 这些虫的一生 , 大多数时间以蛆的形式生活在地下 , 到化蛹出地洞需要7、13或17年 , 出来后翻飞繁殖 , 最多几周就死亡了 。
为什么这些虫要素数年后才出洞呢?据说是为了减少被天敌追杀的概率 。 70年代 , 素数不仅是发明公钥密码算法的基础 , 还是现代许多数学领域里发展的根基 。
公式之美
上世纪初 , 印度的天才数学家Ramanujan , 在剑桥大学见到Hardy之前 , 给Hardy写了一封信 , 内含他发现的等式 。
左边是个无穷的连分式 , 而右边却是个简洁的初等的表达式 。 Hardy看到后说:“它完全击溃了我 , 我之前一点也没有看过这样的东西 , 只有一流的数学家才能写出来!” , 这就是让人眼前一亮的数学 。
下面的例子跟我们的日常生活有关 。 一个自然数n的分割函数 , 是n个物体分配方案的个数 , 比如说n等于2有两种分法;n等于3有三种分法;等n等于4的时候就不是4种分法了 , 而是5种分法;n等于5 , 有7种分法 。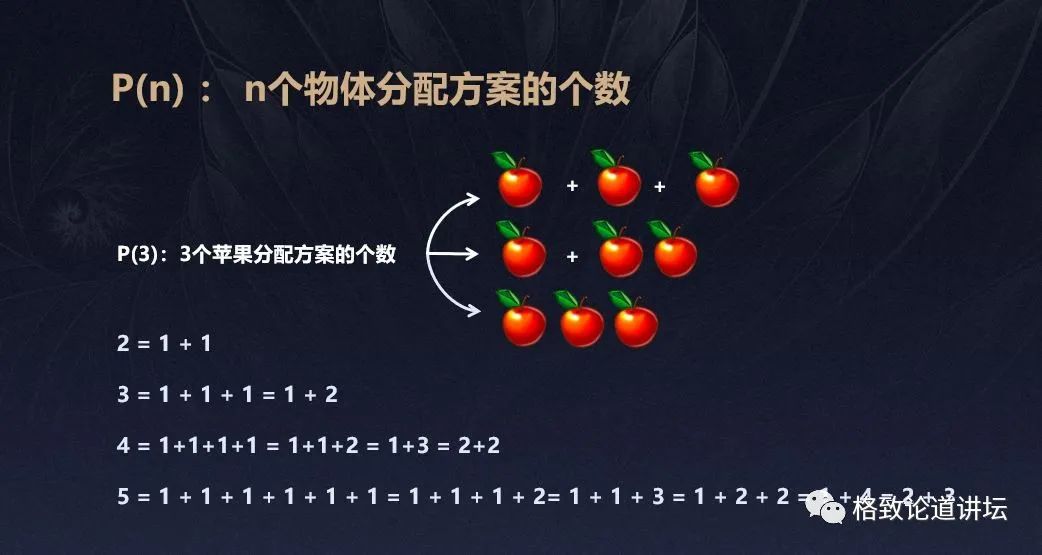
推荐阅读
- 中医刘医师|山竹有“水果皇后” 之美名,每天坚持吃1个,4个好处不请自来
- 数学|六年级数学广角―鸽巢问题到底有多难,一份单元测试卷告诉你答案
- 好玩|历史上的勾股定理,背后那些好玩的事儿
- 青年|邓莎辅导孩子写作业,一道数学题半天解不出来,网友:这题超纲了
- 综艺|网红数学老师VS最狂语文老师,究竟谁更见多识廣?
- 中考;北京卷|北京中考题联系学生生活实际 北斗三号等进入数学题
- 很快|当被问烧脑数学题,郭麒麟很快就算出结果,现实版的“范思辙”吗?
- 伤感|伤感之美,五首冷门诗词邀你月下倚玉阑
- 函数|数学干货丨高中数学错题本该怎样整理?准高三必备(附函数知识点)
- 遇上|综艺 | 《见多识广2》:网红数学老师遇上“最狂”语文老师,究竟谁更见多识广?