数学|数学之美!数学家的这些兴奋点,你能理解吗?( 二 )
我们看一下数字 , P(2)等于2 , P(3)等于3 , P(4)等于5 , P(5)等于7 , P(10)等于42 。 大家看到P(100)已经很大 , 而到P(200)那就更大 。 看了这组数据以后 , 你可能会说增长太快了 , 没法数 , 但是有人会数 。
Hardy和Ramanujan在1918年 , Uspensky在1920年独立证明“当n充分大时 , P(n)与近似号右边的初等函数的值相近 。 同样 , 近看P(n)的数字跳跃的很厉害 , 看不出什么规律 , 远看它却以一个初等函数的规律显示出来 , 这个结果是猜不出来的 。
他们是用了数论里面的圆法 , 经过复杂的计算得到的 , 他们做出了别人难以想象的结果 , 分割函数也常出现在量子物理中 。
数学的“残缺美”
听说过“残缺美”这个词吧?我们不得不想到 , 维纳斯女神的断臂雕像 。
如果不是断臂 , 它只是普通西方女人的雕像 , 谁也记不住 , 可是一断臂 , 让看过的人终生难忘 。 那么数学上有没有这样的事情呢?
1637年费尔马在阅读丢番图《算术》的拉丁文译本 , 写到:“不可能把一个正整数的三次方 , 分成两个正整数的三次方之和;不可能把一个数的四次方 , 写成两个正整数的四次方之和;对正整数的更高次幂也类似 。 我发现了一个奇妙的证明 , 但这个空格太小了 , 写不下 。 ”
这就是所谓的费尔马大定理 。 用公式写就是 , 对大于2的整数n , 不存在正整数abc , 使得a的n次幂加b的n次幂等于c的n次幂 。 其实费尔马自己只证明了n等于4的情形 。 欧拉证明了n等于3的情形 。 1995年 , 由当时在普林斯顿大学的Andrew wiles教授所证明 。 他现在在英国牛津大学 。
由于没有看到费尔马留下的证明 , 人们尝试证明它的过程中发展了代数数论、椭圆曲线理论、Hecke代数理论等 。
如果费尔马真的证明了并把证明留下来 , 那么这些理论的发展很可能延缓 , 所以这就是数学的“残缺美” 。
还有没有解决的数学难题吗?有 。 对我们中国来讲 , 最熟悉的就是哥德巴赫猜测 。
一个大于2的偶数都可以写成两个素数之和 , 这就是所谓的“1加1”问题 。 例如4等于2加2 , 6等于3加3 , 8等于3加5 , 10等于3加7 , 也等于5加5 , 12等于5加7等等 , 人们用计算机验证了所有小于等于4乘10的18次方的偶数 , 结论都对 , 可是到现在为止 , 人们仍然无法证明它 。
1973年 , 我国著名的数学家陈景润证明 , 一个大于2的偶数可以写成两个素数之和 , 或一个素数加上两个素数之积 。 这就解决了所谓的1加2问题 , 这是该方向迄今为止最好的结果 。
除此之外 , 还有一个问题叫做孪生素数猜测 , 存在无穷多个素数p , 使得p+2也是素数 , 这是个千古之谜 。 到2013年 , 华人数学家张益唐证明了存在无穷多个素数 , 使得从p到p加7000万这个区间内也含素数 , 这是数论领域里面一项革命性的工作 。
在这之前人们不知道是否有这样的有限区间存在 , 在这之后格林和陶哲轩等人用张益唐的方法把7000万改到200 , 取得了很大的进展 , 但是离最后的结果2还相差很远 , 算法上还需要改进 。
我们常看到星星 , 可能没注意到有一个多体问题 。 物理学家和数学家一直试图找出相互有引力的n个物体的运动轨迹 , n等于2时 , 已经被约翰·伯努利在17世纪解决;当n大于2时 , 却至今没有解决 。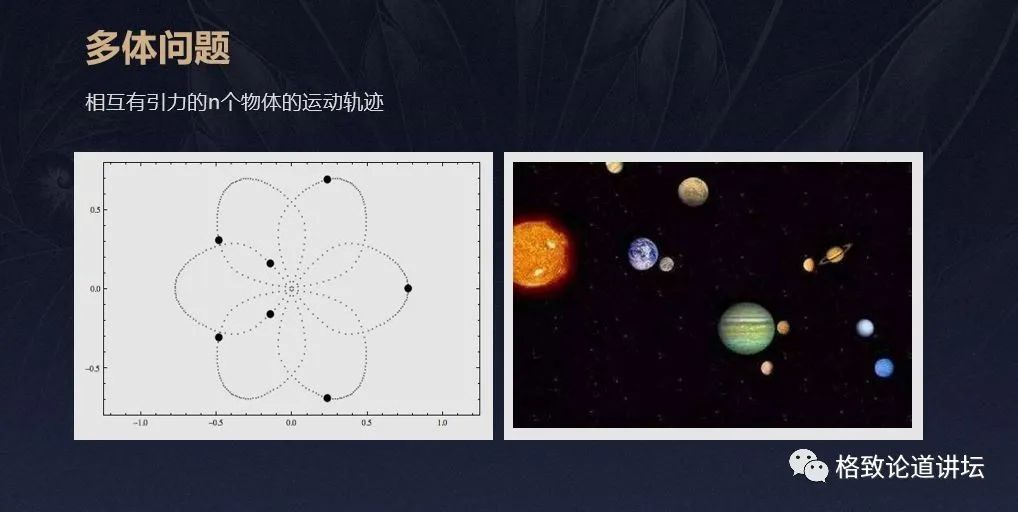
2007年我在解n个物体在一条直线上的特殊模型时 , 发现了具有高斯超几何函数3个基本性质的多元超几何函数 。 在1798年的博士论文中 , 高斯引进了著名的单变元超几何函数 , 它的重要性就是由这三个基本性质导出的 。
【数学|数学之美!数学家的这些兴奋点,你能理解吗?】流体我们都熟悉 , Navier-Stokes方程就是流体力学中基本方程 。
推荐阅读
- 中医刘医师|山竹有“水果皇后” 之美名,每天坚持吃1个,4个好处不请自来
- 数学|六年级数学广角―鸽巢问题到底有多难,一份单元测试卷告诉你答案
- 好玩|历史上的勾股定理,背后那些好玩的事儿
- 青年|邓莎辅导孩子写作业,一道数学题半天解不出来,网友:这题超纲了
- 综艺|网红数学老师VS最狂语文老师,究竟谁更见多识廣?
- 中考;北京卷|北京中考题联系学生生活实际 北斗三号等进入数学题
- 很快|当被问烧脑数学题,郭麒麟很快就算出结果,现实版的“范思辙”吗?
- 伤感|伤感之美,五首冷门诗词邀你月下倚玉阑
- 函数|数学干货丨高中数学错题本该怎样整理?准高三必备(附函数知识点)
- 遇上|综艺 | 《见多识广2》:网红数学老师遇上“最狂”语文老师,究竟谁更见多识广?















