йҮҸеӯҗ|еҺҶеҸІзҡ„з»Ҳз»“дёҺжңҖеҗҺзҡ„дәә | йҮҸеӯҗеӨҡдҪ“дёӯзҡ„е‘җе–ҠдёҺеҪ·еҫЁд№Ӣеӣӣ( дәҢ )
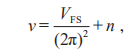
жң¬ж–ҮеӣҫзүҮ
жӯӨеӨ„ ОҪ = N/L2жҳҜзі»з»ҹдёӯзҡ„з”өеӯҗеҚ жҚ®ж•° пјҢ е°ұжҳҜдәҢз»ҙ LГ—Lжҷ¶ж јдёҠж”ҫ N дёӘз”өеӯҗ пјҢ е№іеқҮжҜҸдёӘж јзӮ№дёҠзҡ„з”өеӯҗж•° пјҢ жіЁж„Ҹ ОҪ еҸҜд»ҘдёҚжҳҜж•ҙж•° гҖӮ иҖҢзӯүејҸеҸіиҫ№зҡ„ VFS жҳҜиҙ№зұійқўзҡ„йқўз§Ҝ пјҢ еҶҚйҷӨд»Ҙ(2ПҖ)2е°ұжҳҜе…¶еҚ жӯЈж–№жҷ¶ж јеёғйҮҢжёҠеҢәзҡ„жҜ”дҫӢ гҖӮ жңҖеҗҺдёҖдёӘn жҳҜдёҖдёӘж•ҙж•° пјҢ д№ҹе°ұжҳҜиҜҙеҰӮжһңжҲ‘们иҖғиҷ‘еӨҡеёҰзҡ„зі»з»ҹ пјҢ йӮЈд№ҲйӮЈдәӣеЎ«ж»Ўзҡ„иғҪеёҰе°ұеңЁжҜҸдёӘж јзӮ№дёҠиҙЎзҢ®дёҖдёӘз”өеӯҗ пјҢn дёӘеҚ жҚ®зҡ„иғҪеёҰе°ұиҙЎзҢ® nдёӘз”өеӯҗ пјҢ еҰӮжһңеҸӘиҖғиҷ‘еҚ•еёҰй—®йўҳж—¶иҝҷдёӘ n=0 гҖӮ жүҖд»Ҙ Luttinger е®ҡзҗҶжҢҮеҮәдәҶиҙ№зұіж¶ІдҪ“(еҚідҪҝжҳҜе…·жңүзӣёдә’дҪңз”Ёзҡ„)е…¶з”өеӯҗзҡ„еҚ жҚ®ж•°е’Ңиҙ№зұійқўеҚ еёғйҮҢжёҠеҢәзҡ„жҜ”дҫӢзІҫзЎ®еҜ№еә” гҖӮ иҝҷжҳҜдёҖдёӘеҫҲжңүз”ЁеӨ„зҡ„з»“и®ә гҖӮ
жҲ‘们жқҘзңӢдёҖдёӘе…·дҪ“зҡ„дҫӢеӯҗ гҖӮ еҰӮеӣҫ 1жүҖзӨә пјҢ еӣҫ 1(a)жҳҜдёҖдёӘиҮӘз”ұз”өеӯҗзі»з»ҹзҡ„еёғйҮҢжёҠеҢәе’Ңиҙ№зұійқў пјҢ и“қиүІзҡ„иҙ№зұійқўд№ӢеҶ…дёәз”өеӯҗеҚ жҚ®жҖҒ пјҢ жҢүз…§ Luttinger е®ҡзҗҶ пјҢ е…¶йқўз§Ҝе’Ңж•ҙдёӘеёғйҮҢжёҠеҢәйқўз§Ҝзҡ„жҜ”дҫӢе°ұжҳҜзі»з»ҹзҡ„з”өеӯҗеҚ жҚ®ж•° ОҪ (е°ұжҳҜжҜҸдёӘж јзӮ№дёҠе№іеқҮжңүеӨҡе°‘дёӘз”өеӯҗ пјҢ еҶҚж¬ЎжіЁж„Ҹ пјҢ еҸҜд»ҘдёҚжҳҜж•ҙж•°) гҖӮ 然еҗҺиӢҘиҰҒиҖғиҷ‘зӣёдә’дҪңз”Ёзҡ„ж•Ҳжһң пјҢ жҲ‘们еҸҜд»Ҙи®©зі»з»ҹж„ҹеҸ—еҲ°дёҖдёӘеҸҚй“ҒзЈҒзҡ„дёҚзЁіе®ҡжҖ§ пјҢ еҚіеӣҫдёӯз»ҝиүІзҡ„зҹўйҮҸ Q =(ВұПҖ, ВұПҖ) жүҖзӨә гҖӮ еҪ“еҸҚй“ҒзЈҒй•ҝзЁӢеәҸжңҖз»ҲеҪўжҲҗж—¶ пјҢ зі»з»ҹдјҡиҝӣе…Ҙз”өиҚ·еҜҶеәҰжіўзҡ„йҮ‘еұһжҖҒ пјҢ е…¶иҙ№зұійқўдјҡеҰӮеӣҫ 1(b)жүҖзӨә пјҢ еҺҹжң¬зҡ„еӨ§иҙ№зұійқўеҸҳжҲҗдәҶеӣӣдёӘе°Ҹзҡ„еҸЈиўӢ (pocket) гҖӮ д№ҚдёҖзңӢ пјҢ е·ҰеҸідёӨиҫ№зҡ„иҙ№зұійқўжҳҺжҳҫдёҚзӣёзӯү пјҢ дҪҶжҳҜж•ҙдёӘиҝҮзЁӢдёӯжҲ‘们没жңүж”№еҸҳз”өеӯҗзҡ„еҚ жҚ®ж•° пјҢ жүҖд»ҘжҢүз…§ Luttinger е®ҡзҗҶ пјҢ иҙ№зұійқўе’ҢеёғйҮҢжёҠеҢәзҡ„жҜ”дҫӢдёҚеә”иҜҘеҸҳеҢ– гҖӮ дҪҶжҳҜе°Ҹ pocket еҚ зҡ„жҜ”дҫӢжҳҫ然жҜ”еӨ§иҙ№зұійқўиҰҒе°Ҹ пјҢ иҝҷжҳҜжҖҺд№ҲеӣһдәӢе‘ўпјҹе…¶е®һLuttinger е®ҡзҗҶжҖ»жҳҜеҜ№зҡ„пјҡд»Һеӣҫ 1(a)еҲ°еӣҫ 1(b) пјҢ зі»з»ҹеҸ‘з”ҹдәҶеҜ№з§°жҖ§з ҙзјә пјҢ еӣҫ 1(b)дёӯзҡ„еҸҚй“ҒзЈҒеәҸз”өиҚ·еҜҶеәҰжіўдёҺеӣҫ 1(a)дёӯж— зӣёдә’дҪңз”Ёиҙ№зұіеӯҗе…·жңүдёҚеҗҢзҡ„平移еҜ№з§°жҖ§ пјҢ еҚіеӣҫ 1(b)дёӯ зҡ„зі»з»ҹе®һз©әй—ҙеҺҹиғһеҹәзҹўжҜ”е·Ұиҫ№й•ҝдәҶдёҖеҖҚ пјҢ x ж–№еҗ‘й•ҝдёҖеҖҚ пјҢ y ж–№еҗ‘й•ҝдёҖеҖҚ пјҢ е®һз©әй—ҙзҡ„еҺҹиғһйқўз§Ҝе°ұеӨ§дәҶ4еҖҚ пјҢ еҖ’з©әй—ҙзҡ„еёғйҮҢжёҠеҢәе°ұе°ҸдәҶ4еҖҚ гҖӮ еңЁе°ҸдәҶ4еҖҚзҡ„еёғйҮҢжёҠеҢәдёӯ пјҢ pocket жүҖеҚ зҡ„жҜ”дҫӢе…¶е®һе’ҢеҺҹжқҘзҡ„еӨ§иҙ№зұійқўеңЁеҺҹжң¬зҡ„еёғйҮҢжёҠеҢәдёӯеҚ зҡ„жҜ”дҫӢжҳҜзӣёеҗҢзҡ„ пјҢ д№ҹе°ұжҳҜиҜҙ пјҢ Luttinger е®ҡзҗҶеҜ№дәҺиҙ№зұіж¶ІдҪ“ пјҢ дёҚи®әе…¶иҙ№зұійқўзҡ„еҪўзҠ¶еңЁзӣёдә’дҪңз”ЁдёӢеҰӮдҪ•еҸҳеҢ– пјҢ жҖ»жҳҜжҠҠз”өеӯҗеҚ жҚ®ж•°е’Ңиҙ№зұійқўзҡ„йқўз§Ҝзҙ§зҙ§иҒ”зі»иө·жқҘ гҖӮ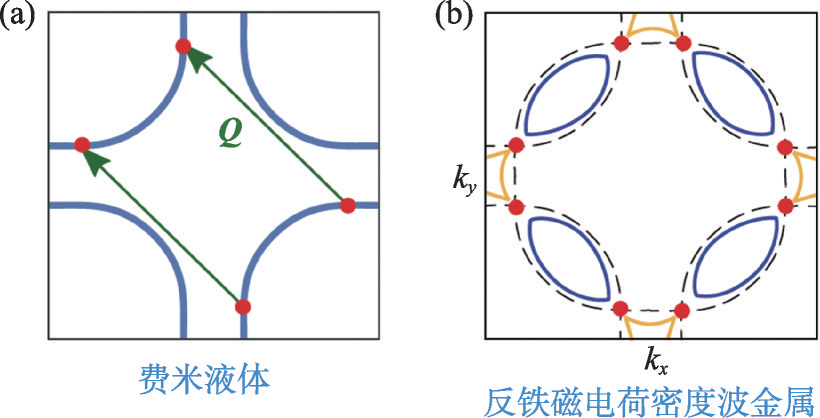
жң¬ж–ҮеӣҫзүҮ
еӣҫ1 Luttinger е®ҡзҗҶе’Ңиҙ№зұійқўзҡ„йқўз§Ҝ (a)дәҢз»ҙжӯЈж–№жҷ¶ж јж— зӣёдә’дҪңз”Ёиҙ№зұіеӯҗе…·жңүдёҖдёӘеӨ§иҙ№зұійқў гҖӮ еҪ“е…¶ж„ҹеҸ—еҲ°еҸҚй“ҒзЈҒзӣёдә’дҪңз”Ёж—¶(еҰӮеңЁ Hubbard жЁЎеһӢдёӯ) пјҢ еҸҚй“ҒзЈҒзҡ„жіўзҹўеҸҜд»Ҙе°Ҷиҙ№зұійқўжҠҳеҸ жҲҗ(b)дёӯзҡ„е°Ҹиҙ№зұійқў пјҢ жҲ–иҖ…еҸ«еҸЈиўӢ(pocket) гҖӮ дёҚи®әжҳҜеӨ§иҙ№зұійқўиҝҳжҳҜе°Ҹиҙ№зұійқў пјҢ е…¶йқўз§Ҝе’ҢеёғйҮҢжёҠеҢәзҡ„жҜ”дҫӢе°ұжҳҜзі»з»ҹдёӯзҡ„з”өеӯҗеҚ жҚ®ж•° пјҢ еҚіLuttingerе®ҡзҗҶ гҖӮ еңЁд»Һ(a)еҲ°(b)зҡ„иҝҮзЁӢдёӯ пјҢ з”өеӯҗеҚ жҚ®ж•°жІЎжңүеҸ‘з”ҹж”№еҸҳ[7]
Luttinger е®ҡзҗҶжҳҜеҰӮжӯӨзҡ„жӯЈзЎ®е’ҢеҘҪз”Ё пјҢ д»ҘиҮідәҺеңЁи®ёеӨҡеҮқиҒҡжҖҒзү©зҗҶеӯҰзҡ„еүҚжІҝй—®йўҳдёӯ пјҢ йғҪеҸҜд»ҘзңӢеҲ°е®ғзҡ„еҪұеӯҗ гҖӮ жҜ”еҰӮйҮҚиҙ№зұіеӯҗзҡ„ Kondo latticeй—®йўҳ пјҢ еҪ“йҮҚиҙ№зұіж¶ІдҪ“еҪўжҲҗж—¶ пјҢ дәә们еҸ‘зҺ°жӯӨж—¶иҙ№зұійқўзҡ„йқўз§ҜеҸҳеӨ§дәҶ пјҢ еӨ§дәҺдәҶзі»з»ҹдёӯе·Ўжёёз”өеӯҗзҡ„иҙ№зұійқў пјҢ еҰӮжһңжҢүз…§ Luttinger е®ҡзҗҶ пјҢ е°ұж„Ҹе‘ізқҖзі»з»ҹдёӯжһ„жҲҗиҙ№зұійқўзҡ„з”өеӯҗж•°еҸҳеӨҡдәҶ гҖӮ жӯӨж—¶ пјҢ еҸӘиҰҒжҠҠеұҖеҹҹзЈҒзҹ©д№ҹи®Ўе…ҘеҲ°з”өеӯҗзҡ„еҚ жҚ®ж•°дёӯ пјҢ з”өеӯҗзҡ„еҚ жҚ®ж•°е°ұе’ҢеҸҳеӨ§еҗҺзҡ„иҙ№зұійқўеңЁеёғйҮҢжёҠеҢәдёӯзҡ„жҜ”дҫӢзӣёзӯүдәҶ[8] гҖӮ е…¶е®һ Oshikawa еҪ“еҲқеҜ№дәҺ Luttinger е®ҡзҗҶзҡ„иҜҒжҳҺ пјҢ е°ұжҳҜз”Ёзҡ„иҝҷдёӘдҫӢеӯҗ пјҢ е‘ҠиҜүдәә们еңЁйҮҚиҙ№зұіж¶ІдҪ“дёӯ пјҢ еӨ§иҙ№зұійқўж—ўжңүе·Ўжёёз”өеӯҗзҡ„иҙЎзҢ® пјҢ д№ҹеә”иҜҘжңүеұҖеҹҹзЈҒзҹ©зҡ„иҙЎзҢ® гҖӮ Luttinger е®ҡзҗҶзңӢжқҘеҰӮжӯӨејәеӨ§ пјҢ иҝһйҮҚиҙ№зұіеӯҗйғҪеҸҜд»Ҙжҗһе®ҡ пјҢ е…¶д»–зҡ„е…іиҒ”зҡ„йҮ‘еұһиҮӘ然д№ҹдёҚеңЁиҜқдёӢ гҖӮ йӮЈд№ҲжҳҜдёҚжҳҜжүҖжңүйҮ‘еұһзҡ„з”өеӯҗеҚ жҚ®ж•°йғҪжҳҜе’Ңиҙ№зұійқўзҡ„йқўз§ҜдёҖдёҖеҜ№еә”е‘ў пјҢ иҝҷжҳҜдёҚжҳҜеҸҲдёҖдёӘвҖңеҺҶеҸІз»Ҳз»“и®әвҖқејҸзҡ„з»“и®әе‘ўпјҹйҡҸзқҖж—¶й—ҙзҡ„еүҚиҝӣ пјҢ жҳҜдёҚжҳҜиҝҳжҳҜдјҡжңүжёҗжёҗ hold дёҚдҪҸзҡ„жғ…еҶөе‘ўпјҹ
иҝҳзңҹжҳҜ пјҢ еңЁеҮқиҒҡжҖҒзү©зҗҶе®һйӘҢдёӯ пјҢ Luttinger е®ҡзҗҶж— жі•и§ЈйҮҠзҡ„жғ…еҶөжҳҜжңүзҡ„ пјҢ е…¶дёӯжңҖи‘—еҗҚзҡ„иҰҒж•°й«ҳжё©и¶…еҜјдҪ“дёӯзҡ„ Fermi arc жҖҒ гҖӮ е°ұжҳҜжҢҮдәә们еңЁй“ңеҹәи¶…еҜјдҪ“зҡ„ж¬ жҺәжқӮеҢәеҹҹйҖҡиҝҮи§’еҲҶиҫЁе…үз”өеӯҗиғҪи°ұи§ӮеҜҹеҲ°жӯӨеӨ„зі»з»ҹзҡ„иҙ№зұійқўдёҚеҶҚжҳҜй—ӯеҗҲзҡ„еңҶеңҲжҲ–иҖ…еҸЈиўӢ пјҢ иҖҢжҳҜеҸҳжҲҗдәҶж–ӯиЈӮзҡ„иҙ№зұіеј§(Fermi arc)[9вҖ”12](йЎәдҫҝиҜҙдёҖеҸҘ пјҢ еңЁй«ҳжё©и¶…еҜјиөқиғҪйҡҷе’Ңиҙ№зұіеј§зҡ„е®һйӘҢеҸ‘зҺ°иҝҮзЁӢдёӯ пјҢ еҮ дҪҚеҚҺдәәе®һйӘҢзү©зҗҶеӯҰ家йғҪеҒҡеҮәдәҶйҮҚиҰҒзҡ„иҙЎзҢ® пјҢ [9вҖ”12]иҝҷеҮ зҜҮж–ҮзҢ®е°ұжҳҜзҺ°еңЁдёӯеӣҪ科еӯҰйҷўзү©зҗҶз ”з©¶жүҖдёҒжҙӘз ”з©¶е‘ҳе’Ңж–ҜеқҰзҰҸеӨ§еӯҰзҡ„жІҲеҝ—еӢӢж•ҷжҺҲж—©е№ҙзҡ„е·ҘдҪң пјҢ еҜ№дәҺе…іиҒ”з”өеӯҗйўҶеҹҹзҡ„еҸ‘еұ•еҪұе“Қж·ұиҝң) гҖӮ еӣҫ2(a)дёәй“ңеҹәи¶…еҜјз©әз©ҙеһӢжҺәжқӮзҡ„зӨәж„Ҹзӣёеӣҫ гҖӮ еҰӮеӣҫ 2(b)жүҖзӨә пјҢ еңЁж¬ жҺәжқӮеҢәеҹҹ( p = 0.1жҺә жқӮ пјҢ з”өеӯҗеҚ жҚ®ж•° ОҪ = 0.9) пјҢ и§’еҲҶиҫЁе…үз”өеӯҗи°ұзңӢеҲ°зҡ„дёҚжҳҜзәўиүІзҡ„й—ӯеҗҲеҸЈиўӢ пјҢ иҖҢжҳҜж–ӯиЈӮзҡ„еј§зәҝпјӣиҖҢеҰӮеӣҫ 2(c)жүҖзӨә пјҢ еҪ“зі»з»ҹеҲ°дәҶиҝҮжҺәжқӮеҢәеҹҹ(
жҺЁиҚҗйҳ…иҜ»
- еҫ·еӣҪ| еұұдёңдёҺеҫ·еӣҪпјҡжңүзқҖй•ҝд№…еҺҶеҸІзҡ„з»ҸжөҺдјҷдјҙ
- з”өеҪұ|еҺҶеҸІдёҠе…ЁзҗғзҘЁжҲҝжңҖй«ҳзҡ„еҚҒйғЁз”өеҪұжҺ’иЎҢжҰңпјҢе“ӘйғЁжҳҜдҪ жңҖе–ңж¬ўзҡ„з”өеҪұпјҹ
- жҢҮзә№|з”ҹзү©иҜҶеҲ«жҠҖжңҜпјҡеҺҶеҸІгҖҒйЈҺйҷ©е’ҢжңӘжқҘ
- гҖҗзҲұйӣҶеҫ®гҖ‘еҸҲжҳҜйҮҸеӯҗзӮ№дё“еҲ©пјҒиҝҷ家公еҸёжӯЈи®ЎеҲ’иө·иҜүдёүжҳҹзҲұйӣҶеҫ®2020-07-20 17:14:320йҳ…
- еҺҶеҸІи§ЈеҜҶеқҠ|еұұиҘҝе®ҒжӯҰжңүвҖңиҜЎејӮвҖқжӮ¬жЈәпјҢжёёдәәеҸҜд»Ҙд»ҺжЈәдҪ“зҡ„зјқйҡҷпјҢзӘҘи§ҶеҲ°йҮҢйқўдёңиҘҝ
- 硬件|еҸҲжҳҜйҮҸеӯҗзӮ№дё“еҲ© Nanocoе…¬еҸёжӯЈи®ЎеҲ’иө·иҜүдёүжҳҹ
- еҚҺеӨ©иҜҙзҫҺйЈҹ|йә»дёҺиҫЈе®ҢзҫҺз»“еҗҲзҡ„йҮҚеәҶзҒ«й”…пјҢдёҖдёӘең°еҹҹзҡ„зү№иүІпјҢдёҖдёӘеҺҶеҸІзҡ„дј жүҝ
- ејҖж’ӯ|гҖҠеҰӮжһңеӣҪе®қдјҡиҜҙиҜқгҖӢ第дёүеӯЈејҖж’ӯпјҢзңӢеҺҶеҸІдёҺзҺ°д»ЈеҰӮдҪ•ж“ҰеҮәеҲ«ж ·зҒ«иҠұ
- ејӢиҜҙеҺҶеҸІ|ж№–еҢ—дёҖиҖғз”ҹеӣ иҮӘеҲӣйңёж°”姓ж°Ҹиө°зәўпјҢжҲ–жҲҗе…ЁеӣҪе”ҜдёҖпјҢдј—дәәеҘҪеҘҮе’ӢдёҠжҲ·еҸЈ
- зІҫеҚҺ|еҸӨжі•е·Ҙиүәдҝ®зј®пјҒйҰҷеұұе°ҶйҮҚзҺ°жё…д№ҫйҡҶж—¶жңҹеҸӨж°ҙзі»еҺҶеҸІеҺҹиІҢ







![[еҚҒзӮ№иө„и®Ҝ]з®ҖзҹӯжҙӢж°”пјҢи®©дәәдёҖи§ҒеҖҫеҝғпјҒпјҢ2020жңӢеҸӢеңҲжңҖзҒ«зҡ„еҝғжғ…иҜҙиҜҙ](https://imgcdn.toutiaoyule.com/20200420/20200420101938102246a_t.jpeg)









